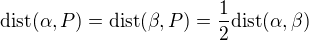Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2019 10:07
- stuart clark

- Příspěvky: 1015
- Reputace: 7
number of plane
If  are
are  distinct points in a space such that no three are collinear and points are not colpanar
distinct points in a space such that no three are collinear and points are not colpanar
Then the number of plane that are in the space and each of which is equidistant from  is
is
Offline
#2 05. 01. 2019 15:10 — Editoval jardofpr (05. 01. 2019 15:42)
#3 05. 01. 2019 17:08 — Editoval check_drummer (05. 01. 2019 17:16)
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: number of plane
"Máte úhel beta." "No to nemám."
Offline
#4 08. 01. 2019 14:27
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: number of plane
tHANKS ↑ jardofpr:↑ check_drummer:
Offline
 and
and 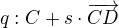
 giving the equation
giving the equation 
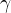 is not known
is not known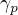 for which the line
for which the line 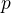 lies in the plane
lies in the plane 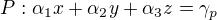
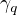 such that line q lies in the plane
such that line q lies in the plane 
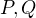 are parallel since they share normal vector, let be
are parallel since they share normal vector, let be 
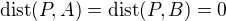 ,
, 
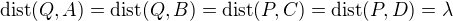
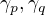 gives us equations for planes
gives us equations for planes  parallel to
parallel to 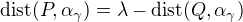
 to
to  and the right side decreases from
and the right side decreases from 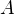 the point in first half-space and
the point in first half-space and 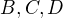 points in the second half-space
points in the second half-space and for sure there is unique plane
and for sure there is unique plane  going through
going through  between those two where
between those two where