Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 01. 2019 10:47
Teorie množin
Ahoj, snažím se vyřešit tento úkol, ale jsem bezradná :/
Je možné sestrojit v rovině množinu vzájemně se neprotínajících se písmen T mohutnosti kontinua? A písmen N?
Napadlo mě, že když T vepíšu do trojúhelníka, tak aby každá nožička protínala jednu stranu trojúhelníka a dám pravidlo, že se nesmí trojúhleníky dotýkat pak je úkol vyřešen. To stejné bych udělala i s písmenem N, které bych vepsala do čtverce. Bohužel jsem pouze převedla problém neprotínajících se písmen na neprotínající se trojúhelníky/čtverce a nevím co s tím.
Děkuji za jakoukoli radu :)
Offline
- (téma jako vyřešené označil(a) Nika01)
#2 14. 01. 2019 15:07 — Editoval Rumburak (16. 01. 2019 12:45)
Re: Teorie množin
↑ Nika01:
Ahoj.
Otevřený čtverec v rovině opatřené kartéskou soustavou souřadnic můžeme vnímat jako kartéský součin
(1)  , kde
, kde  .
.
Každému ze čtverců (1) pevně přiřaďme nějakou uspořádanou dvojici ![kopírovat do textarea $[r, s]$](/mathtex/39/392451c096081af1ae14c51f90c088c1.gif) racionálních čísel, která je v něm
racionálních čísel, která je v něm
obsažena. Že takové zpbrazení exitsuje, plyne jednak z faktu, že každý otevřený interval obsahuje rac. číslo,
a jednak z axiomu výběru.
Předpokládejme navíc, že uvažované čtverce (1) jsou voleny tak, aby byly po dvou disjunktní. Potom příslušné
usp. dvojice ![kopírovat do textarea $[r, s]$](/mathtex/39/392451c096081af1ae14c51f90c088c1.gif) budou navzájem různé, tudíž jich bude nejvýše spočetně mnoho (jak plyne z faktu, že
budou navzájem různé, tudíž jich bude nejvýše spočetně mnoho (jak plyne z faktu, že
množina  všech racionálních čísel je spočetná, při čemž tuto vlastnost nutně má i množina
všech racionálních čísel je spočetná, při čemž tuto vlastnost nutně má i množina  ).
).
Odtud je k řešení Tvého problému už jen krůček.
EDIT. V tomto úsudku jsem se poněkud unáhlil.
Offline
#3 14. 01. 2019 17:13
Re: Teorie množin
Chápu-li to dobře pak ctverec je zadán 8 racionálními čísly a to je spočetné, takže množina čtverců je spočetná a tím i množina písmen N?
Takže u písmene T, si také řeknu že mám trojújelník v rovině opatřený kartéskou soustavou souřadnic. Každému trojuhelníku přiřadím uspořádanou dvojici ![kopírovat do textarea $[x, y]$](/mathtex/fa/fabd3d28b8c416add9ccc1ce034e36e9.gif) , tak aby trojuhelníky byly disjunktní. Tím pádem je trojuhelník zadán 6 racionálními čísly (ty vrcholy) a to je spočetné, pak je spočetná množina trojuhelníků a tím pádem i písmen T. ?
, tak aby trojuhelníky byly disjunktní. Tím pádem je trojuhelník zadán 6 racionálními čísly (ty vrcholy) a to je spočetné, pak je spočetná množina trojuhelníků a tím pádem i písmen T. ?
Offline
#4 15. 01. 2019 11:08 — Editoval Rumburak (15. 01. 2019 13:22)
Re: Teorie množin
↑ Nika01:
Jak je to s písmenem T, jsem ještě spolehlivě nerozluštil, avšak připadá mi, že to dopadne stejně jako
s těmi čtverci.
Pokusím se ukázat, jak by to bylo s písmenem L.
Základní polohou písmene L nazvěme množinu

(doporučuji nakreslit si obrázek). Tuto množinu můžeme libovolně posunovat ve směru vektoru  ,
,
čímž získáme množiny
(1)  ,
,
kde  probíhá množinu všech reálných čísel (co je míněno zápisem (1), je snad jasné).
probíhá množinu všech reálných čísel (co je míněno zápisem (1), je snad jasné).
Množiny (1) jsou po dvou disjunktní a tvoří soubor mohutnosti kontinua. Zauvažuj, zda by se něco takového
nedalo udělat s písmenem N.
Offline
#5 15. 01. 2019 18:45 — Editoval check_drummer (15. 01. 2019 18:45)
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Teorie množin
Ahoj. Měl bych zajímavou hypotézu - pokud je ten zkoumaný útvar "čára", která se "větví" (nedefinuju přesně co to znamená, ale asi je to jasné), tak existuje v rovině jen spočetně mnoho jejích disjunktních kopií (včetně jejich zmenšení). Nevím, jestli to platí, ale pokud ano, tak klíč bude v okolí bodu větvení...
"Máte úhel beta." "No to nemám."
Offline
#6 15. 01. 2019 19:21 — Editoval jardofpr (15. 01. 2019 20:24)
Re: Teorie množin
ahojte
možno cesta? kedysi som niečo podobné riešil, v skratke:
1.) predpoklad že existuje nespočítateľná množina disjunktných  -čok v rovine
-čok v rovine
2.) pre každé  z tejto množiny existuje štvorec s racionálnou dĺžkou strany a s racionálnym stredom
z tejto množiny existuje štvorec s racionálnou dĺžkou strany a s racionálnym stredom
tak že toto  z neho trčí von kolmo cez tri jeho strany
z neho trčí von kolmo cez tri jeho strany
trojice racionálnych čísel sú spočítateľné takže musí byť pre nejakú jednu konkrétnu trojicu
štvorec ktorý patrí k nespočítateľne veľa  -čkam
-čkam
3.)  -čko rozdeľuje štvorec na 3 oblasti, v každej z nich existuje bod s racionálnymi súradnicami
-čko rozdeľuje štvorec na 3 oblasti, v každej z nich existuje bod s racionálnymi súradnicami
potom pre nejakú trojicu bodov s racionálnymi súradnicami je nespočítateľne veľa  ktoré
ktoré
rozdeľujú štvorec na také tri oblasti že v každej je jeden z týchto troch bodov
4.) teraz sa ukáže že ak sú len dve také rôzne  tak sa vnútri štvorca pretnú
tak sa vnútri štvorca pretnú
↑ check_drummer: tiež neviem či to platí ale vidím to podobne, akonáhle sa z toho nedá urobiť
úsečka ale je to niečo "komplikovanejšie" - t.j. s vetvením ako píšeš;
intuitívne toto isté nevieme urobiť so znakmi bez "vetvenia", lebo tieto vieme k sebe uložiť "ľubovoľne blízko",
podobne ako urobil ↑ Rumburak: v jeho príspevku
Offline
#7 16. 01. 2019 11:02 — Editoval Rumburak (16. 01. 2019 11:04)
Re: Teorie množin
↑ jardofpr:
Také zdravím.
Zamyslet se nad tím intuitivně není těžké, ale dát tomu nějakou obecně platnou formální stránku už bude horší.
Aby bylo možno získat nespočetně mnoho navzájem disjunktnách kopií, nesmí se originál větvit ani sám sebe
protínat, jak se zdá. Ale je otázka, zda to stačí. Oriinál nejspíš ani nesmí mít "příliš mnoho zatáček". Kompletní
vyřešení problému bych prozatím viděl na Abelovu cenu. :-).
Offline
#8 16. 01. 2019 11:55
Re: Teorie množin
↑ Rumburak:
Teorii množin absolutně nerozumím, ale snad jsem to pochopila z toho písmene L :)
Takže u písmene N, to dám do čtverce v rovině opatřeném kartéskou soustavou souřadnic:
 , kde
, kde  .
.
A tuto množinu můžu libovolně posunovat tak jak u písmena L?
Akorát si nejsem jisá tím posunutím, prvně jsem si říkala, že by to mohlo být 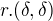 ale to by pak nebyly disjunktní ne? tak jsem uvažovala že kdybych dala, že r se nesmí rovnat 1, pak by se to nepotkalo.
ale to by pak nebyly disjunktní ne? tak jsem uvažovala že kdybych dala, že r se nesmí rovnat 1, pak by se to nepotkalo.
takže bych ta množina vypadala: 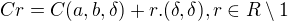
nebo určit místo  něco jiného, pro něž platí
něco jiného, pro něž platí  .
.
S tím písmenem T, stále nevím. V knize Vilenkin-Vyprávění o množinách je prý návod ae nepobírám to :/ každopádně je to přes trojuhelníky.
Offline
#9 16. 01. 2019 14:02 — Editoval Rumburak (17. 01. 2019 11:32)
Re: Teorie množin
↑ Nika01:
Jednodušší by bylo postavit to základní "N" poněkud šikmo, např. jako lomenou čáru ABCD,
kde A= [0, 0], B = [1,2], C = [2,0], D = [3,2], a celek pak posouvat ve směru osy y, tj. přičítáním
vektoru 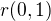 , kde
, kde  by probíhalo množinu všech reálných číslel.
by probíhalo množinu všech reálných číslel.
Ještě poznámka: I když zde pracujeme s množinami (což ostatně činíme i v ostatních oblastech
matematiky), do teorie množin bych tyto problémy nezařazoval. Podle mne spadají spíše do
geometrie či do matematické analýzy nebo topogie.
PS. Ten postup podle oné knihy by mne docela zajímal.
Offline
#10 16. 01. 2019 17:37
Re: Teorie množin
↑ Rumburak:
pokud postavím to N šikmo, tak pak už nepoužívám ty čtverce, cos mi radil hned na začátku nebo ano?
když to nechám teda jako šikmé, pak by ta množina byla 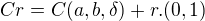 ?
?
tady je odkaz na tu knihu, patří to pod kapitolu Osmičky v rovině a je to na straně 90-92
https://1url.cz/@vilenkin
Offline
#11 17. 01. 2019 12:35 — Editoval Rumburak (17. 01. 2019 15:04)
Re: Teorie množin
↑ Nika01:
Možná si nerozumíme. Jde o to, že existují 2 situace:
První situace - např. s písmeny L , V, W, Z, N - se vyznačuje tím, že kopii disjunktní s originálem
můžeme dostat posunutím originálu (ve vhodném směru) již o libovolně malou délku.
Ta "šikmost" je tam proto, aby byl jednodušší vektor posunutí. Mohli bychom "šikmost" nepožadovat,
ale pak bychom museli vzít složitější (tj. patřičně "šikmý") vektor posunutí - například u písmen L, N.
Ve druhé situaci - s písmeny A, B, K, P, H , O a j. nebo se čtvercem - už libovolně malá délka posunutí
ke získání disjunktní kopie nestačí (v žádném směru). Ten příklad od Tebe ještě projdu.
Do té knížky se rád podívám . :-)
Offline
#12 17. 01. 2019 20:49 Příspěvek uživatele Nika01 byl skryt uživatelem Nika01. Důvod: nedopasný příspěvek
#13 17. 01. 2019 20:57
Re: Teorie množin
↑ Rumburak:
Díky, myslím, že mi tohle ujasnilo problém :)
Takže písmeno N napíšu jako lomenou čáru L, která se skládá z vrcholů písmene N (vrchol A,B,C,D), pak množina prvního písmene N je: ![kopírovat do textarea $L=\{A,B,C,D\} kde A=[0,0] B=[1,2] C=[2,0] D=[3,2]$](/mathtex/ab/ab6c73e131deb263311e155d99c89373.gif) Posunutím o vektor
Posunutím o vektor 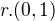 kde
kde 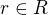 vznikne množina všech neprotínajících se písmen N, která lze zapsat
vznikne množina všech neprotínajících se písmen N, která lze zapsat  Je to takhle správně?
Je to takhle správně?
K tomu písmenu T, kdybych to dala do rovnostranného trojúhleníku o straně  , a posunu to o vektor (a,0) tak se trojuhleníky nepotkají ne? Akorát si lámu hlavu jak zapsat rovnostranný trojúhelník do jako nějakou množinu v kartézském souřadnicovém systému.
, a posunu to o vektor (a,0) tak se trojuhleníky nepotkají ne? Akorát si lámu hlavu jak zapsat rovnostranný trojúhelník do jako nějakou množinu v kartézském souřadnicovém systému.
Offline
#14 18. 01. 2019 11:33 — Editoval Rumburak (18. 01. 2019 11:40)
Re: Teorie množin
↑ Nika01:
To s písmenem N je správně. Důležité při tom je, že
1) "počet" všech takto získaných množin 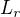 je roven "počtu" všech reálných čísel
je roven "počtu" všech reálných čísel
(odborně říkáme, že množina  má mohutnost kontinua) ,
má mohutnost kontinua) ,
2) pro dvě různá reélná 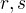 , ať jsou jakkoliv blízká , je
, ať jsou jakkoliv blízká , je 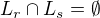 .
.
Pro písmeno T můžeme analogickou konstrukcí zajistit splnění podmínky 1, ale nikdy nezajistíme
splnění podmínky 2.
Příkladem z praxe jsou plastové kelímky na limonádu ve tvaru komolého kužele, jemuž chybí
větší podstava, které můžeme nejefektivněji poskládat tím, že vložíme jeden do druhého.
Pokud by tyto kelímky měly "ucho", pak by to nešlo.
Offline
#15 20. 01. 2019 21:41
#16 22. 01. 2019 10:19
Re: Teorie množin
↑ Nika01:
Přesněji:
Množina neprotínajících se T sice existuje, avšak ne taková, aby měla mohutnost kontinua.
Je to dáno tím, že dvě různá T nelze k sobě přiblížit dostatečně úsporně (tj. zcela těsně ) -
vždy bude mezi nimi nějaká nevyužitá část plochy ve tvaru otevřené množiny.
Offline
#17 25. 01. 2019 18:32
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Teorie množin
Rumburak napsal(a):
↑ Nika01:
Je to dáno tím, že dvě různá T nelze k sobě přiblížit dostatečně úsporně (tj. zcela těsně ) -
vždy bude mezi nimi nějaká nevyužitá část plochy ve tvaru otevřené množiny.
Ahoj, no ono to platí i třeba pro písmeno L - ať zvolíš dvě libovolná, vždy se mezi ně vejde otevřená množina, spíš by bylo lepší to popsat třeba tak, že u T neexisuje spojitá trasnformace převádějící jedno T na druhé taková, že všechny "meziútvary" T jsou disjunktní.
"Máte úhel beta." "No to nemám."
Offline
#18 28. 01. 2019 10:36
Re: Teorie množin
↑ check_drummer:
To je vlastně pravda. Vyjádřit to pomocí té spojité transformace mne bohuřžel nenapadlo.
Offline


![kopírovat do textarea $K=\{k_a; k_a = \{ [x,y]; x^2+y^2=a^2\}, a > 0\}$](/mathtex/d7/d7cbe6e80015e71e04f83f2e7750b86d.gif)