Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 01. 2019 19:00
- Arabidopsis

- Zelenáč
- Příspěvky: 8
- Škola: Gymnázium Svitavy
- Pozice: student
- Reputace: 0
Objem rotačního tělesa - určitý integrál
Dobrý den,
potřebovala bych se ujistit, že rozumím správně výpočtu objemu rotačního tělesa.
Zadání je: vypočtěte objem rotačního tělesa vzniklého otáčením omezené rovinné oblasti kolem osy x. Rovinná oblast je ohraničena grafy funkcíy = xe^x, y = x a přímkou x = 1.
Vím, že objem rotačního tělesa by se měl počítat jako: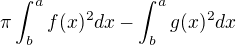
Potom tedy:
Vychází mi 
Postupuji správně?
Moc děkuji!
Offline
#2 24. 01. 2019 19:06
Re: Objem rotačního tělesa - určitý integrál
↑ Arabidopsis:
Zdravím,
ve výpočtu chybí závorka:
chybí závorka: 
Ve výsledku ti chybí 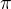 , jinak by to mělo být správně.
, jinak by to mělo být správně.
Offline
#3 24. 01. 2019 19:11
- Arabidopsis

- Zelenáč
- Příspěvky: 8
- Škola: Gymnázium Svitavy
- Pozice: student
- Reputace: 0
Re: Objem rotačního tělesa - určitý integrál
Ano, jsem zmatkař. Děkuju moc!
Pěkný večer.
Offline
#4 24. 01. 2019 19:38
Re: Objem rotačního tělesa - určitý integrál
↑ Arabidopsis:
Vztah pro objem můžeš upravit na tvar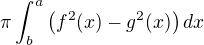
Offline
