Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 03. 2019 17:42
Logická algebra - příklad
Přeji dobrý den,
několikátým dnem bojuji se závěrem jednoho příkladu. Jedná se o: 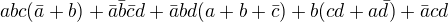
Dostal jsem se k výsledku 
Dle výsledků ve sbírce (Kantnerová - Sbírka příkladů z číslicové techniky) je výsledek
Dokážete mne prosím nasměrovat, jak dále postupovat?
Děkuji
Offline
#2 16. 03. 2019 11:12
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Logická algebra - příklad
↑ noskins:
Ahoj, možná to bude hodně neformální: Jde tedy o to, zda je možné člen abc vypustit.
Proměnné a,b,c,d mohou nabývat jen hodnoty 0 nebo 1? Pokud ano, tak pokud bude abc splněno, tak bude tedy a=b=c=1, což ovšem znamená (jak lze snadno zjistit - ať už je d=0 nebo d=1), že některý z nevynechaných členů bude roven 1 - a tedy i celý výraz bude roven 1.
Pokud jsou a,b,c členy nějaké obecné algebry, tak možná pomůže pdoobná úvaha.
Tak abych to shrnul - máš to správně, ale jde to ještě více zjednodušit.
"Máte úhel beta." "No to nemám."
Offline
#3 16. 03. 2019 11:34
Re: Logická algebra - příklad
Ahoj,
děkuji, včera jsem nad tím ještě dumal a vykoumal jsem to, co píšeš.
Vliv na výsledek funkce bude mít pouze: 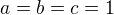
v případě vynechání členu, když a, b, c = 1, pak = závislost na hodnotě d
= závislost na hodnotě d
a zároveň  = závislost na hodnotě d negativní,
= závislost na hodnotě d negativní,
takže při a,b,c = 1 je výsledná hodnota funkce vždy rovna logické hodnotě 1, jelikož je závoslé na hodnotě d, popř. d negativní.
Vnitřně si to takhle nějak vysvětlím, jde mi spíše o jisté matematické vyjádření, popř. jaký Booleův zákon využít.
Offline
#4 17. 03. 2019 09:35
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Logická algebra - příklad
↑ noskins:
Nevím, zda jeto nějaký zákon, ale spíš jde o jakousi závislost členu abc na ostatních členech výrazu. A pokdu je tato závislost přítomna, pak je závislý člen nadbytečný.
"Máte úhel beta." "No to nemám."
Offline