Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 05. 2019 16:19 — Editoval NeuRotiCk (14. 05. 2019 16:20)
Diferenciální rovnice
Dobrý den, mám tu jeden příklad na diferenciální rovnice, chtěl bych se jen zeptat, jestli jsem postupoval správně:
Nalezněte obecné řešení:y’y=x 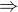 y’=x/y
y’=x/y


To je podle mě všechno, kamarádka to právě že chtěla řešit substitucí, ale to mi přijde jako blbost, když tam mám jenom jeden člen, substituce je podle mě zbytečná.
Předem děkuji za odpověď
Offline
- (téma jako vyřešené označil(a) NeuRotiCk)
#2 14. 05. 2019 16:28
Re: Diferenciální rovnice
↑ NeuRotiCk:
Dobrý den,
snad jen drobnost:
Máte: 
a po úpravě dostanete:  kde:
kde: 
Offline
#5 14. 05. 2019 17:12
#7 14. 05. 2019 17:23
Re: Diferenciální rovnice
↑ NeuRotiCk:
Dobrý den,
OK, dopočtěte C dle vašeho zadání 
a dosaďte do rovnice, čímž dostanete jedno partikulární řešení pro zadané parametry.
Offline
#9 14. 05. 2019 17:32
#11 14. 05. 2019 18:02
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)




 nevím proč sem to dvakrát opsal špatně. Děkuju za opravu.
nevím proč sem to dvakrát opsal špatně. Děkuju za opravu.![kopírovat do textarea $\sqrt{2\cdot [(1/4)^{2}/2+c]}=\sqrt{65}/4\Rightarrow 2\cdot [(1/16)/2+c]$](/mathtex/1a/1a5eafbcc46fd6014ce4ae7bfac88e76.gif)


 což by zhruba vycházel tomu vašemu
což by zhruba vycházel tomu vašemu 



