Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 05. 2019 23:07 Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#3 24. 05. 2019 00:41
Re: Konvergence integrálu
↑ zzzz1:
Zřejmě v tomto případě budeš muset zkoumat konvergenci na intervalech (0;K) a (K; nekonečno)
V případě (K; nekonečno) bych využila spojitosti funkce a toho, že 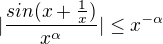 a zkoumala tak konvergenci majoritního integrálu pro učité hodnoty alfa.
a zkoumala tak konvergenci majoritního integrálu pro učité hodnoty alfa.
V případě intervalu (0;K) použít limitní srovnávací kriterium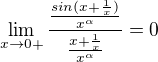 (věta o sevřené limitě, spojitost funkcí na (0;K>, kladnost funkce uvedené ve jmenovateli limity) a zkoumat konvergenci integrálu pro určitá alfa
(věta o sevřené limitě, spojitost funkcí na (0;K>, kladnost funkce uvedené ve jmenovateli limity) a zkoumat konvergenci integrálu pro určitá alfa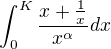
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline