Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 08. 06. 2019 06:14
Re: goniometrie
↑ Ikaruss:
Zdravím,
nezlob se, ale tolik chyb v zápise na jednom místě!
1. Jesliže , potom v intervalu 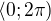 (na jedné kružnici) je
(na jedné kružnici) je 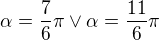
2. Máš spočítat 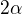 . Jak se násobí zlomky?
. Jak se násobí zlomky? 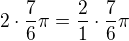 A teď buď vynásobíš čitatele a vynásobíš jmenovatele a pak pokrátíš, nebo pokrátíš 2 proti 6 a vynásobíš. Dostaneš
A teď buď vynásobíš čitatele a vynásobíš jmenovatele a pak pokrátíš, nebo pokrátíš 2 proti 6 a vynásobíš. Dostaneš  . Podobně spočítej i
. Podobně spočítej i 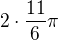
3. Obě hodnoty 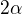 nemají základní velikost - přesahují jednu kružnici. Takže musíš tu základní velikost najít. Kolikrát se vejde jedna kružnice do
nemají základní velikost - přesahují jednu kružnici. Takže musíš tu základní velikost najít. Kolikrát se vejde jedna kružnice do  ? Vypočet je
? Vypočet je 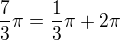 . Základní velikost úhlu
. Základní velikost úhlu 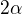 je
je  . Podobně pro druhý úhel.
. Podobně pro druhý úhel.
4. Jestliže 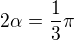 , potom
, potom  , nikoli
, nikoli  !!!
!!!
Úlohu lze počítat i bez výpočtů úhlů s použitím goniometrických vzorců 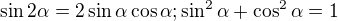 .
.
Offline

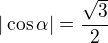 a dosazením do prvního vztahu máš výsledek. Musíš také sledovat, ze kterých kvadrantů jsou úhly
a dosazením do prvního vztahu máš výsledek. Musíš také sledovat, ze kterých kvadrantů jsou úhly 