Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 08. 2019 19:51
- lenkavlkova
- Příspěvky: 36
- Reputace: 0
Teorie množin
Ahoj,
prosim, poradil byste mi nekdo s timto prikladem? Vubec si s nim nevim rady :-( Dekuji moc
Offline
#2 20. 08. 2019 13:42 — Editoval Rumburak (20. 08. 2019 13:44)
Re: Teorie množin
↑ lenkavlkova:
Ahoj. Vysvětleme si to metajazykem (t.j. nikoliv formálním jazykem).
P(X) - tzv. potenční třída třídy X - je třída všech takových podtříd třídy X, které jsou zároveň
množinami.
Máme dokázat větu
(V) Jestliže třídy X, Y jsou spolu exvivalentní, potom jsou spolu ekvivalentní i třídy P(X), P(Y).
Jinými slovy: předpokládáme, že existuje bijekce F mezi třídami X, Y a na základě tohoto předpokladu
hledáme bijekci H mezi třídami P(X), P(Y). Nalezením takové bijekce H bude důkaz hotov.
V hranaté závorce je nápověda, jak bijekci H zavést: Množině x, která je prvkem třídy P(X) , přiřadíme
množinu y , na niž se zobrazí množina x při zobrazení F.
Offline
#3 21. 08. 2019 20:56
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: Teorie množin
Ahoj, proč obrácená implikace neplatí? Existuje protipříklad, nebo důkaz, že ta implikace nejde dokázat? :-)
"Máte úhel beta." "No to nemám."
Offline
#4 22. 08. 2019 07:50
Re: Teorie množin
↑ check_drummer:↑ Rumburak:Ahoj. Nie je obrátená implikácia (zovšeobecnená) hypotéza kontinua? (Neviem. Iba sa pýtam)
MATH IS THE BEST!!!
Offline
#5 22. 08. 2019 10:24 — Editoval Rumburak (22. 08. 2019 10:27)
Re: Teorie množin
↑ jarrro:
Ahoj. Soustředil jsem se pouze na tu impliklaci z leva do prava, která není obtížná.
O té obrácené implikaci mne zatím nic nenapadá (obávám se, mé znalosti z teorie
množin či tříd nejsou dostatečně hluboké), mohl by tam snad hrát roli axiom výběru,
ale to jen hádám.
Offline
#6 04. 07. 2020 16:17
Re: Teorie množin
Tá obrátená implikácia sa v ZFC nedá ani dokázať ani vyvrátiť. (Ale platí, ak predpokladáme GCH.)
Pridám nejaké linky:
* When  implies
implies 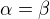 (
( cardinals)
cardinals)
* Equality of Cardinality of Power Set
* Do sets, whose power sets have the same cardinality, have the same cardinality?
* Does  imply
imply 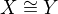 without assuming the axiom of choice?
without assuming the axiom of choice?
Offline

