Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Algebra - tělesa: co znamená následující symbol v této větě?
#1 25. 08. 2019 20:43
- dominiksep
- Příspěvky: 54
- Reputace: 0
Algebra - tělesa: co znamená následující symbol v této větě?
Ahoj,
potřeboval bych pomoci s vysvětlením významu následující věty:
Buďte S rozšíření tělesa T,  . Je-li a algebraický nad T, potom existuje izomorfismus okruhů
. Je-li a algebraický nad T, potom existuje izomorfismus okruhů ![kopírovat do textarea $\varphi : T[x]/<f> \rightarrow T[a]$](/mathtex/7e/7ee84e7fe0b6b46b4d2975c0ee0d9c2a.gif) ,
,
kde f je miminmálmí polynom a. Přitom ![kopírovat do textarea $T \hookrightarrow T[x]/<f>$](/mathtex/31/313d67ae34c8aa674901332a20dfc0b0.gif) ,
, ![kopírovat do textarea $T \subset T[a]$](/mathtex/03/03b07940fa4988f44ad509d1eaf25f96.gif) a platí
a platí  .
.
Jaký je význam symbolu 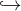 v tomto kontextu? Spolužák mi řekl, že si myslí, že je to vnoření (tedy zkráceně existence prostého zobrazení ve směru té šipky), druhý zase, že si to rovnou psal jako podmnožiny...
v tomto kontextu? Spolužák mi řekl, že si myslí, že je to vnoření (tedy zkráceně existence prostého zobrazení ve směru té šipky), druhý zase, že si to rovnou psal jako podmnožiny...
Pokud by to bylo vnoření, jaká je jeho definice v tomto kontextu?
Díky.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Algebra - tělesa: co znamená následující symbol v této větě?

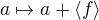 , kde
, kde 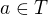 .
.