Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definiční obor funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 11. 2019 17:45
Definiční obor funkce více proměnných
Dobrý den,
prosím o radu s určením definičního oboru funkce: 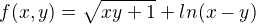
Mám dvě podmínky a to: 
Druhá podmínka lze upravit na tvar  . To znamená mít polorovinu určenou přímkou y=x a polorovina by byla směrem "dolů".
. To znamená mít polorovinu určenou přímkou y=x a polorovina by byla směrem "dolů".
S první podmínkou mám problém. Lze upravit na tvar 
A dále rozdělit na tři případy x=0, x>0 a x<0
a) x=0
Pokud by bylo x=0, tak potom y může nabývat jakékoliv hodnoty, neboť 0*něco je vždy větší než -1. Graficky by to byla polopřímka, která by vycházela z bodu [0,0] a splynula by s osou y.
b) x>0
Lze dále upravit na:  .
.
c) x<0
Také upravit na poslední zmiňovaný tvar.
Graficky jsem případ b) a c) znázornila na obrázku z Geogebry. 
Definiční obor by pak měl být znázorněn na obrázku červeně. 
Můžete mi prosím poradit, zda postupuji správně a pakliže ano, tak jak mám zapsat zápisem definiční obor funkce?
Děkuji!
Offline
- (téma jako vyřešené označil(a) Johana16)
#2 01. 11. 2019 18:06
Re: Definiční obor funkce více proměnných
↑ Johana16:
Ahoj. Takze napriklad bod [-1,-3] nepatri do definicniho oboru funkce f?
Offline
#4 01. 11. 2019 18:34 — Editoval Al1 (01. 11. 2019 20:36)
Re: Definiční obor funkce více proměnných
↑ Johana16:
Zdravím,
Ad b) správný zápis má být 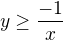
Ad c) dělíš záporným číslem, musíš obrátit znaménko nerovnosti, dostaneš 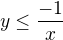
Offline
#6 01. 11. 2019 19:34
Re: Definiční obor funkce více proměnných
↑ Johana16:
Ano, jen si uvědom, že červená a modrá část roviny je jedna množina. To až budeš hledat průnik.
Offline
#8 01. 11. 2019 19:52
Re: Definiční obor funkce více proměnných
↑ Johana16:
Vezmi část roviny zelenomodrou a zelenočervenou.
Offline
#11 01. 11. 2019 20:35 — Editoval Al1 (01. 11. 2019 20:37)
Re: Definiční obor funkce více proměnných
↑ Johana16:
Ne.![kopírovat do textarea $D(f)=\{[x,y]\in E_{2}: (y<x) \wedge(xy\ge-1)\}$](/mathtex/6b/6b7facd9590eeb57e643fee7ddde5f05.gif)
V tvé množině by chybêla zelenomodrá část.
Offline
#13 01. 11. 2019 21:21
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definiční obor funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)


![kopírovat do textarea $D(f)=\{[x,y]\in E_{2}: (y<x) \wedge (y>\frac{-1}{x})\}$](/mathtex/3c/3c4c6832c3fed2e6e05545c142ab2056.gif) ?
?