Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 11. 2019 00:28 — Editoval vanok (23. 11. 2019 08:58)
Polynomy
Pozdravujem
Najdite vsetki komplexne polynomy  take, ze
take, ze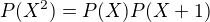
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 23. 11. 2019 08:33
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Polynomy
↑ vanok:
AHoj, někde ti tam chybí závorky(a). Nemá to být 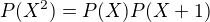 ?
?
"Máte úhel beta." "No to nemám."
Offline
#3 23. 11. 2019 08:59
Re: Polynomy
Ahoj ↑ check_drummer:,
Dakujem, preklep opraveny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 24. 11. 2019 20:26
Re: Polynomy
Najprv, mozte konstatovat, ze konstatne polynomy  a
a  vyhovuju.
vyhovuju.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 25. 11. 2019 11:33 — Editoval check_drummer (25. 11. 2019 20:23)
#6 25. 11. 2019 13:58 — Editoval vanok (14. 01. 2020 16:21)
Re: Polynomy
Pozdravujem ↑ check_drummer:,
Polynomy ktore vyhovuju su 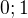 a aj take ak a je koren polynomu P, tak aj
a aj take ak a je koren polynomu P, tak aj  je. Co to znamena?
je. Co to znamena?
A mozeme nast aj ine korene?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 25. 11. 2019 15:38
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Polynomy
↑ vanok:
Ahoj, aha, ještě je nutno uvažovat kořen s absolutní hodnotou 0, tj. 0. Zamyslím se nad tím.
"Máte úhel beta." "No to nemám."
Offline
#8 25. 11. 2019 20:32
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Polynomy
↑ vanok:
Trošku jsem upravil řešení. Taky by se dalo brát že k může být i 0 a pak můžeme polynom 1 vynechat :-)
"Máte úhel beta." "No to nemám."
Offline
#9 26. 11. 2019 07:07 — Editoval vanok (26. 11. 2019 07:10)
Re: Polynomy
Pozdravujem ↑ check_drummer:,
Mala poznamka.
Len pripomeniem, ze polynom jednej premennej je definovany je formalne definvany na komutativnom okruhu A ako postupnost skoro stale nulova prvkov A. ( podrobnejsie pozri fr. a engl. wikipediu)
A prakticky, treba byt velmi opatrny a netreba miesat “ formalny” polynome (algebricky object) a jeho asociovanu funkciu polynom.
Priklad: polynome 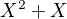 na
na 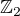 nie nulovy, aj ked jeho asociovana funkcia polynom je nulova.
nie nulovy, aj ked jeho asociovana funkcia polynom je nulova.
I ked za urcitych okolnosti mozme vyhodne pouzit ich vzajomne vlasnosti.
Napr.
Formalny polynom  nie je definovany.
nie je definovany.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 26. 11. 2019 08:22
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Polynomy
↑ vanok:
Ahoj. A je povoleno využít Základní větu algebry?
"Máte úhel beta." "No to nemám."
Offline
#11 26. 11. 2019 09:49 — Editoval vanok (26. 11. 2019 09:51)
Re: Polynomy
↑ check_drummer: ,
Dobra otazka.
Co je dolezite , je treba vediet kde presne pracujes ( myslim o teoriu v akej pracujes).
Moja poznamka, to je len ti ukazat, ze formalne polynomy; formalne serie ... su uzitocne studovat. A to moze pomoct aj co sa tyka ich asociovanych funkcii a aj opacne. ( algebra a a analyza mozu byt intimne viazane).
Ozaj, studovali ste, ked si bol student do hlbky formalne algebricke objekty?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 26. 11. 2019 17:02
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Polynomy
↑ vanok:
Ahoj, algebru jsme měli asi 2 semestry, k tomu asi 2 semestry lineární algebru. Moc do hloubky to nebylo (byl jsem na oboru informatika), něco víc jsem si o tom pak přečetl sám, ale to bylo asi 10 let po škole. :-)
Ale formální algebry mají hodně blízko k logice, je dána nějaká teorie, axiomy, a z nich se odvozují další vlastnosti. Je tam obecně méně prostoru na názornost než třeba v analýze, ale to už je spíš věc názoru a věc konkrétního tématu.
"Máte úhel beta." "No to nemám."
Offline
#13 26. 11. 2019 21:55
Re: Polynomy
Ahoj ↑ check_drummer:,
To tak celkom nie je, o sa tyka nazornosti. Ale asi na nematematickych smeroch taka algebra sa uci vo velmi minimalnej forme. No urcite je toho dost pre ludi v takych odboroch.
No ty sa snazis ist do hlbky. To preto napredujes.
Pridam tu, len co budem mat cas este jedno riesenie daneho problemu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 14. 01. 2020 18:10 — Editoval vanok (16. 01. 2020 04:01)
Re: Polynomy
Dam tu ↑ vanok: riesenie problemu. ( akoze to zatial nikto kompletne neriesil).
Nech a je koren polynomu P.
Akoze, mnozina korenov polynomu P je konecna, tak l‘aplikacia 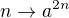 nie je injektivna. Preto existuju dve prirodzene cisla m a n, take, ze
nie je injektivna. Preto existuju dve prirodzene cisla m a n, take, ze 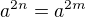 . Ak
. Ak  , tak
, tak  .
.
Z toho mame, ze mame alebo a=0 alebo  . ( a komplexne cislo).
. ( a komplexne cislo).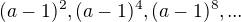 su korene P, co vyzaduje
su korene P, co vyzaduje 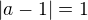 alebo
alebo 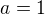 .
.
Preto jedine mozne korene P su 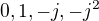 ( skutocne
( skutocne 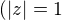 a
a  alebo
alebo  . )
. )
Tiez mame 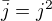 co znamena, ze
co znamena, ze 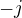 a
a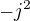 maju rovnaju multiilicitu v rozklade P.
maju rovnaju multiilicitu v rozklade P.
Vidime, ze 
Co znamena, ze 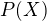 je formy
je formy 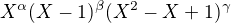 ( pre vhodne
( pre vhodne 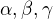 , ktore nam ostava upresnit)
, ktore nam ostava upresnit)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 15. 01. 2020 18:50 — Editoval vanok (15. 01. 2020 18:51)
Re: Polynomy
Tak teraz phrepokladajme, ze 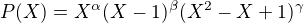 .
.
To nam da, 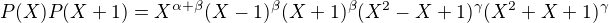
(Tiez vidime, ze  ).
). 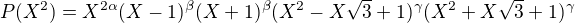 .
.
Akoze mame jednoznacnost faktorizacie na irreduktibiline polynomy tak nevyhnutne 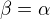 a
a  .
.
Cize 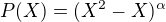 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

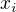 . Potom pravá strana rovnosti má kořeny
. Potom pravá strana rovnosti má kořeny  a levá strana má kořeny
a levá strana má kořeny 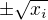 a množiny kořenů polynomů na obou stranách rovnosti se rovnají. Nechť kořen levé strany s maximální absolutní hodnotou je
a množiny kořenů polynomů na obou stranách rovnosti se rovnají. Nechť kořen levé strany s maximální absolutní hodnotou je  , potom pokud je tato absolutní hodnota větší než 1, tak je
, potom pokud je tato absolutní hodnota větší než 1, tak je  a kořen
a kořen 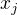 je roven nějakému
je roven nějakému 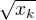 - a tento poslední kořen má větší absolutní hodnotu než
- a tento poslední kořen má větší absolutní hodnotu než  ) by musel mít argument
) by musel mít argument  (pro nějaké k celé), ovšem mezi kořeny by musela být i
(pro nějaké k celé), ovšem mezi kořeny by musela být i 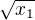 a i hodnota
a i hodnota  a lze ukázat, že nakonec získáme kořen, který nemá absolutní hodnotu 1, což je spor.
a lze ukázat, že nakonec získáme kořen, který nemá absolutní hodnotu 1, což je spor.