Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 12. 2019 16:28
Re: báze vektorového prostoru
↑ Daniel99:
1. Aké sú vlastnosti bázy vektoroveho priestoru?
2. Úlohu som presunul, bolo zle zaradená – ide o štandartnú úlohu, na ktorej nie nič zaujímavé.
Offline
#3 27. 12. 2019 16:53 — Editoval Daniel99 (27. 12. 2019 16:53)
Re: báze vektorového prostoru
No, báze je každá linaérně nezávislá skupina vektorů v daném vektor. prostoru.
Zkusil jsem to hodit do matice a vyšlo mi, že pokud
p=1 nebo p=2, tak budou vektory lin.nezávislé a tím pádem by právě tohle měl být výsledek.
Je to tak, nebo je to úplná blbost?↑ vlado_bb:
Offline
#4 27. 12. 2019 17:27
Re: báze vektorového prostoru
↑ Daniel99: Nepocital som to, ale uz len geometricka predstava mi hovori, ze takych  by malo byt nekonecne vela. Co samozrejme neznamena, ze pre
by malo byt nekonecne vela. Co samozrejme neznamena, ze pre 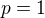 pripadne
pripadne 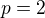 nejde o bazu, ale zadavatelia ulohy mali asi na mysli urcenie mnoziny VSETKYCH takych
nejde o bazu, ale zadavatelia ulohy mali asi na mysli urcenie mnoziny VSETKYCH takych  .
.
Offline
#5 27. 12. 2019 17:40
Re: báze vektorového prostoru
Daniel99 napsal(a):
No, báze je každá linaérně nezávislá skupina vektorů v daném vektor. prostoru
Ne. Napr. vektory (1,0,0), (0,1,0) jsou lin. nezavisle, ale bazi netvori. To jen pro doplneni.
Nejlepe udelas, kdyz sem ten svuj postup posles. Tak nejak se mi zda, ze v nem bude hned nekolik chyb (p=0 je na prvni pohled specialni pripad).
Offline
#7 28. 12. 2019 10:47
Re: báze vektorového prostoru
↑ Daniel99:
Jak jsem říkal, vidím několik problémů.
Ten hlavní je, že to mazácky "házíš do matice", aniž bys u toho přemýšlel, jakou soustavu vlastně řešíš a proč. Proto pak také nejsi z výsledku schopen ani poznat, které případy odpovídají lineární závislosti, a které lineární nezávislosti. Podívej se na definici lineární nezávislosti a také může pomocí tento starý příspěvek, ve kterém jsem to rozepisoval.
Další problém je, že děláš numerické chyby, konkrétně po první úpravě vpravo dole nemá být  .
.
Navíc i kdyby tvé úpravy byly správně, tak by z nich určitě neplynulo nic zvláštního pro p=2 a p=1 - v těch případech je matice regulární, jako ve většině jiných. Zajímavé by byly případy p=-2 a p=0.
Offline
#8 30. 12. 2019 12:44
Re: báze vektorového prostoru
Ale nám preci jde o to, aby byla matice regularni, ne?
To znamena, ze kdyz pak vypocitam jeji determinant, tak ten se nesmi rovnat nule.
Vyslo mi pak, ze vysledkem jsou vsechna p, ktera se nerovnaji 0 a 2.
Offline
#9 30. 12. 2019 12:50 — Editoval LukasM (30. 12. 2019 13:34)
Re: báze vektorového prostoru
↑ Daniel99:
No, háček je jenom v tom, že když je regulární, tak jsou vektory lineárně NEzávislé. A druhý háček je v tom, že obě tebou nalezená řešení jsou špatně (v tom smyslu, že nejsou ničím speciální). Nevím, jak jinak to mám ještě napsat.
Edit: resp aby to bylo jasne. Ano, 2 a 0 jsou resenim puvodniho zadani, v tech pripadech jsou vektory LZ. Predtim jsem komentoval tvuj postup. Ted jak to ctu jsem to nenapsal jasne.
Offline


