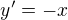Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 28. 12. 2019 14:50
Re: Soustava diferenciálních rovnic
Jediná opravdu diferenciální rovnice je ta první, x' = -x
Ty zbylé dvě už diferenciální rovnice nejsou, je to jen čisté integrování - takže to vůbec není potřeba řešit jako soustavu. Stačí vyřešit tu první, a pak už jen integrovat.
Offline
#4 17. 01. 2021 11:42
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1047
- Reputace: 18
- Web
Re: Soustava diferenciálních rovnic
Soustavy diferenciálních rovnic jsou též na mém webu www.tucekweb.info
sekce vyšší matematika
Offline