Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 21. 01. 2020 14:01
Re: Rekurentní vyjádření posloupnosti
↑↑ Ferdish:
Promiň, mluvíš o něčem úplně jiném. Já jsem kritizoval ten hybrid, ne rekurentní zadání. A u rekuretního zadání fakt nemusíš počítat všechny členy, pokud znáš ten předchozí.
Na výpočet n-tého členu není rekurentní vyjádření určeno, k tomu je vzorec pro n-tý člen.
Offline
#27 21. 01. 2020 14:05
Re: Rekurentní vyjádření posloupnosti
↑↑ jarrro:
A k čemu je tedy hybridní vyjádření dobré? Nemá výhody ani rekuretního vyjádření, ani vzorce pro n-tý člen. Jediné, kde bych to toleroval, jsou ty případy, kdy základní vyjádření nelze provést.
Offline
#28 21. 01. 2020 14:08
Re: Rekurentní vyjádření posloupnosti
↑↑ misaH:
Bez urážky (vidím, že jsi lehce v afektu), ale pojmu rekurentní vyjádření není jasné spíš tobě. Přečti si ten výřez a promysli si ho.
Rekurentní vyjádření neobsahuje samotné n, nýbrž předchozí členy.
Vzorec pro n-tý člen neobsahuje předchozí členy, nýbrž n.
Hybrid obsahuje obojí.
Offline
#29 21. 01. 2020 14:36 — Editoval jarrro (21. 01. 2020 14:37)
Re: Rekurentní vyjádření posloupnosti
↑ surovec:kde je v texte na obrázku od↑↑ misaH: napísané, že predpis nemôže závisieť od indexu?
A ako by si postupoval pri úlohe
"Nech 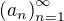 je postupnosť daná rekurentne predpisom
je postupnosť daná rekurentne predpisom
Určte 12345678910. člen tejto postupnosti." ?
MATH IS THE BEST!!!
Offline
#30 21. 01. 2020 16:46
Re: Rekurentní vyjádření posloupnosti
↑ jarrro:
To myslíš vážně??? To už si snad děláš srandu? Tak znova: to, co jsi napsal, je rekurentní vyjádření. Rekurentní vyjádření slouží k dopočítání členu POMOCÍ PŘEDCHOZÍCH ČLENŮ, nikoliv pro dopočítání členu s konkrétním indexem!!!
Na dopočítání členu s konkrétním indexem slouží vzorec pro n-tý člen!
Navíc vůbec nechápu, jakou to má souvislost se zde řešeným názorovým rozporem, že vzorec obsahující zároveň  i předchozí členy není rekurentním vyjádřením...
i předchozí členy není rekurentním vyjádřením...
Offline
#31 21. 01. 2020 16:58
Re: Rekurentní vyjádření posloupnosti
Myslim, ze ↑ surovec: chce povedat asi tolko, ze rekurentna formula v tvare  je niekedy vyhodnejsia ako rekurentna formula v tvare
je niekedy vyhodnejsia ako rekurentna formula v tvare  . V tom ma pravdu. On by zasa mohol vziat na vedomie, ze jedno aj druhe JE rekurentna formula.
. V tom ma pravdu. On by zasa mohol vziat na vedomie, ze jedno aj druhe JE rekurentna formula.
Offline
#33 21. 01. 2020 17:14
Re: Rekurentní vyjádření posloupnosti
↑ vlado_bb:
Ne, to jsem nechtěl říct. Chtěl jsem říct, že formule typu  je prakticky k ničemu. A zároveň trvám na tom, že pokud je tam n, tak už to není rekurentní, protože z předchozích členů pomocí ní nespočítám nic, pokud nebudu zároveň vědět, kolikátý člen to je.
je prakticky k ničemu. A zároveň trvám na tom, že pokud je tam n, tak už to není rekurentní, protože z předchozích členů pomocí ní nespočítám nic, pokud nebudu zároveň vědět, kolikátý člen to je.
Pokud je hybrid k něčemu dobrý (jednoznačně lepší než existující "striktně rekurentní" vyjádření či vzorec pro n-tý člen), uveď takový příklad a mně nebude dělat problém přiznat, že jsem se v této věci pletl.
Mimochodem, ještě k "hybridnímu" příkladu, který jsem uvedl  . Rekurentní vyjádření je
. Rekurentní vyjádření je  a vzorec pro n-tý člen je prostě
a vzorec pro n-tý člen je prostě  . Pomocí nich úlohy a) i b) vypočítám snadno, hybridem nespočítám nic...
. Pomocí nich úlohy a) i b) vypočítám snadno, hybridem nespočítám nic...
Offline
#34 21. 01. 2020 17:19
- misaH
- Příspěvky: 13460
Re: Rekurentní vyjádření posloupnosti
↑ surovec:
Ako že "hybridom" nespočítaš nic?
Nedokážeš vyrátať napríklad 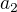 ?
?
To naozaj?
Offline
#35 21. 01. 2020 17:33 — Editoval Ferdish (21. 01. 2020 18:13)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Rekurentní vyjádření posloupnosti
EDIT (k téme, po prečítaní ↑ surovec:): Aritmetická postupnosť (AP) a geometrická postupnosť (GP) sú tiež postupnosti s rekurentným predpisom: nejaký člen je vyjadrený pomocou iného, a nemusí to byť nutne ten predošlý, ale ktorýkoľvek iný.
U AP však nestačí poznať iba ten "iný člen", musí sa k nemu niečo pripočítať, a síce vhodný násobok tzv. diferencie
 ktorá určuje rozdiel medzi ľubovoľnými dvoma susednými členmi AP.
ktorá určuje rozdiel medzi ľubovoľnými dvoma susednými členmi AP.Ako veľký násobok to bude, závisí od rozdielu indexov člena ktorý hľadáme (nazvem
 ) a "iného" člena ktorého pri výpočte používame (
) a "iného" člena ktorého pri výpočte používame (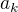 ), teda na veľkosti
), teda na veľkosti 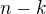 .
.Zároveň nutnou podmienkou je, aby sme poznali hodnotu aspoň jedného člena hľadanej AP (nie nutne
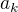 ) Takže vo všeobecnosti pre
) Takže vo všeobecnosti pre  -tý člen AP platí
-tý člen AP platí
a ako vidíme, neplatí striktne
 ale
ale  .
.Obdobne u GP, tam sa však k tomu "inému členu" nič nepripočítava, ale dochádza k jeho násobeniu vhodnou mocninou tzv. kvocientu
 , ktorý určuje pomer dvoch za sebou idúcich členov GP (člen s vyšším indexom v čitateli). A znova mocnina závisí na indexoch hľadaného člena a "iného člena" a znova musíme poznať hodnotu aspoň jedného člena GP. Využijem označenie z predošlého odstavca a môžem písať, že pre
, ktorý určuje pomer dvoch za sebou idúcich členov GP (člen s vyšším indexom v čitateli). A znova mocnina závisí na indexoch hľadaného člena a "iného člena" a znova musíme poznať hodnotu aspoň jedného člena GP. Využijem označenie z predošlého odstavca a môžem písať, že pre  -tý člen GP platí
-tý člen GP platí
takže ani tu striktne neplatí
 ale
ale  .
.Alebo asi jeden z najznámejších príkladov rekurentne zadanej postupnosti - Fibonacciho postupnosť.
Členy tejto postupnosti sú dané súčtom hodnôt dvoch predchádzajúcich členov, pričom prvé dva členy postupnosti
 . Takže pre členy Fibonacciho postupnosti máme
. Takže pre členy Fibonacciho postupnosti máme
takže ani tu nemáme
 ale pre zmenu
ale pre zmenu  . A toto skrátka nemôžeš poprieť...
. A toto skrátka nemôžeš poprieť... Offline
#36 21. 01. 2020 20:12 — Editoval misaH (21. 01. 2020 20:13)
- misaH
- Příspěvky: 13460
Re: Rekurentní vyjádření posloupnosti
↑ Ferdish:
Ahoj - škoda času. Trvá na tom...
Z hnusného hybridu nespočíta (nevyráta) nič, čo už teda - komu niet rady, tomu niet pomoci...
Offline
#37 22. 01. 2020 00:04 Příspěvek uživatele moab byl skryt uživatelem moab. Důvod: Mylná reakce...
#40 22. 01. 2020 07:36 — Editoval jarrro (22. 01. 2020 07:45)
Re: Rekurentní vyjádření posloupnosti
Zase je pravda, že úloha typu nejaký člen má hodnotu  určte nasledujúci je pri "hybride" najrýchlejšie riešiteľná (snáď) vyriešením diferenčnej rovnice a zistením indexu.
určte nasledujúci je pri "hybride" najrýchlejšie riešiteľná (snáď) vyriešením diferenčnej rovnice a zistením indexu.
Len by som bol zvedavý kde sa vyskytuje znalosť člena bez znalosti jeho indexu (pri riešení seriózneho matematického/fyzikálneho problému alebo priamo v praxi teda nie umelo vytvorené úlohy typu ↑↑ surovec:).
Netvrdím, že taký prípad nemôže nastať.
Mimochodom z autonómnej (rekurencia nezávisí na indexe) diferenčnej rovnice vypočítaš člen z daným indexom aj bez riešenia rekurzie (proste budeš dostatočne dlho dosadzovať)(tak tisto ako aj pri neautonómnej )
MATH IS THE BEST!!!
Offline
#41 22. 01. 2020 09:12
Re: Rekurentní vyjádření posloupnosti
↑ Ferdish:
Aha, tak to se omlouvám, už se tady v tom člověk ztrácí...
Offline
#43 22. 01. 2020 11:31
Re: Rekurentní vyjádření posloupnosti
Pozdravujem,
Poznamka.
Pochopitelne toto cvicenie ma viacej ciest k rieseniu. Co je pripad situacii, ktore nevedu k linearnym recurenciam.
Pre zabavu, mozme vyhodne pouzit, ze dana relacia sa da vyjadrit vdaka trojuholnikovim cislam, ktore su « dokladne » studovane ( cf Fermat, Gauss).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#44 22. 01. 2020 17:51
- check_drummer

- Příspěvky: 5173
- Reputace: 106
Re: Rekurentní vyjádření posloupnosti
surovec napsal(a):
↑↑ jarrro:
A k čemu je tedy hybridní vyjádření dobré? Nemá výhody ani rekuretního vyjádření, ani vzorce pro n-tý člen. Jediné, kde bych to toleroval, jsou ty případy, kdy základní vyjádření nelze provést.
Ahoj. Vyskytuje-li se ve vyjádření i index n, pak se takové vyjádření standardně řadí mezi rekurentně zadané posloupnosti.
K čemu může být dobré? K mnoha věcem - např. proto, že explicitní vyjádření i "čistě" rekurentní
mohou být dány příliš složitými vzorci, a tedy to, které využívá předchozí člen i index n, může být dostatečně jednoduché. Nebo sice nemusí být takové vyjádření jednoduché, ale může být snadnější s ním analyticky pracovat, odvodit pomocí něj nějaké vhodné vlastností té posloupnosti, apod.
Každopádně odsuzovat takové vyjádření apriori není znakem matematické kreativity a otevřenosti.
"Máte úhel beta." "No to nemám."
Offline