Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 01. 2020 18:02
- Queensberry

- Zelenáč
- Příspěvky: 4
- Škola: Pf prešov
- Pozice: Student
- Reputace: 0
Pravdepodobnosť
Dobrý deň kto by mi vedel pomocť s prikladom: Rozhodnite či platí implikácia P(A) + P(B) =1 tak P ( AUB ) = množina moźnych vysledkov
Offline
#2 29. 01. 2020 19:22
Re: Pravdepodobnosť
↑ Queensberry: je cislo a nie mnozina. Ale asi tusim, o co ti ide. Pouvazuj o tomto:
je cislo a nie mnozina. Ale asi tusim, o co ti ide. Pouvazuj o tomto: - nahodne vybrate realne cislo z intervalu
- nahodne vybrate realne cislo z intervalu ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif) je cele
je cele  - nahodne vybrate realne cislo z intervalu
- nahodne vybrate realne cislo z intervalu ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif) je iracionalne.
je iracionalne.
Offline
#3 29. 01. 2020 21:41 — Editoval Ferdish (29. 01. 2020 21:41)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravdepodobnosť
↑ vlado_bb:
To nie je dobrý príklad...aj keď je na danom intervale nespočítateľne veľké množstvo čísiel, tu určite neplatí P(A) + P(B) = 1.
Offline
#4 29. 01. 2020 23:18
#5 30. 01. 2020 00:05
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravdepodobnosť
↑ vlado_bb:
Podľa mňa
kde - počet všetkých celých čísiel v intervale
- počet všetkých celých čísiel v intervale ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif)
 - počet všetkých iracionálnych čísiel v intervale
- počet všetkých iracionálnych čísiel v intervale ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif)
 - počet všetkých reálnych čísiel v intervale
- počet všetkých reálnych čísiel v intervale ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif)
Offline
#6 30. 01. 2020 07:25 — Editoval vlado_bb (30. 01. 2020 09:41)
#7 30. 01. 2020 09:37 — Editoval Ferdish (30. 01. 2020 09:39)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravdepodobnosť
↑ vlado_bb:
Nie som matematik, takže hlbšia teória ide trochu mimo mňa. Prečo by pp javu že z intervalu ![kopírovat do textarea $[0,100]$](/mathtex/f5/f5cf82e35e85966d6cf05ce7062f89f4.gif) náhodne vyberiem práve celé číslo by mala byť rovná 1, čo znamená jav istý? Čo ak mnou náhodne vybrané číslo bude racionálne, teda nebude vyhovovať ani javu A ani javu B?
náhodne vyberiem práve celé číslo by mala byť rovná 1, čo znamená jav istý? Čo ak mnou náhodne vybrané číslo bude racionálne, teda nebude vyhovovať ani javu A ani javu B?
Navyše intuícia mi hovorí, že  a
a  nebudú "rovnaké" nekonečná, pretože
nebudú "rovnaké" nekonečná, pretože  obsahuje práve aj neuvažované racionálne čísla.
obsahuje práve aj neuvažované racionálne čísla.
Offline
#8 30. 01. 2020 09:40 — Editoval vlado_bb (30. 01. 2020 09:45)
Re: Pravdepodobnosť
↑ Ferdish:Nie je rovna jednej, ale nule. Ak ma nejaky jav nulovu pravdepodobnost, neznamena to, ze nemoze nastat, tu mame priklad takej situacie.
V minulom prispevku som mal zamenene  a
a  , uz som to opravil.
, uz som to opravil.
A 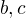 su sice kardinality roznych mnozin, ale pre ucely pravdepodobnosti je dolezita ich miera a ta je rovnaka.
su sice kardinality roznych mnozin, ale pre ucely pravdepodobnosti je dolezita ich miera a ta je rovnaka.
Offline
#9 30. 01. 2020 09:48
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravdepodobnosť
↑ vlado_bb:
:-)
Offline
#10 19. 05. 2020 12:45
Re: Pravdepodobnosť
Dobrý deň kto by mi vedel pomocť s prikladom:
1. Vypočítajte pravdepodobnosť pri hode jednou hracou kockou, ktorá má na stenách čísla: 1, 2, 3, 4, 5, 6. Zapíšte výsledky do zošita v tvare zlomku v základnom tvare takto: 2/3.
a,Na kocke padne číslo 1. Pravdepodobnosť je:
b,Na kocke padne číslo 5. Pravdepodobnosť je:
c,Na kocke padne párne číslo. Pravdepodobnosť je:
d,Na kocke padne nepárne číslo. Pravdepodobnosť je:
e,Na kocke padne číslo deliteľné trojkou. Pravdepodobnosť je:
f,Na kocke padne číslo deliteľmé dvojkou. Pravdepodobnosť je:
g,Na kocke padne číslo väčšie ako 2. Pravdepodobnosť je:
h,Na kocke padne číslo menšie ako 6. Pravdepodobnosť je:
i,Na kocke padne číslo väčšie ako 2 a menšie ako 5. Pravdepodobnosť je:
j, Na kocke padne párne číslo menšie ako 4. Pravdepodobnosť je:
Offline
#11 19. 05. 2020 13:45
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Pravdepodobnosť
↑ Jakub00b:
Na kostce je 6 čísel 1 je tam jednou
pravděpodobost, že padne jednička je : 1/6
To samé, že padne 5: 1/6
Kolik je sudých čísel mezi 1 až 6
Kolik je lichých čísel mezi 1 až 6
Kolik čísel je dělitelných 3 mezi čísly 1 až 6
Kolik čísel je dělitelných 2 mezi čísly 1 až 6
Kolik čísel je větších jak 2 mezi čísly 1 až 6
Kolik čísel je menších než 6 mezi čísly 1 až 6
Kolik je sudých čísel menších jak 4 mezi čísly 1 až 6
Stačí takto?
Nikdo není dokonalý
Offline
 ?
? .
.![kopírovat do textarea $P(B)=\frac{\lambda\{[0,100]\cap (R \setminus Q)\}}{\lambda \{[0,100]\}}=1$](/mathtex/7c/7c93f8d9e7b8aa743de4e131059f24f1.gif)
![kopírovat do textarea $P(A)=\frac{\lambda\{[0,100]\cap Z\}}{\lambda \{[0,100]\}}=0$](/mathtex/e9/e9ee07935e55761b18253da826d7c1b0.gif)
 je Lebesgueova miera na
je Lebesgueova miera na  .
.