Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 04. 2020 23:13
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
normalne rozdelenie
ahojte, vedeli by ste mi odporucit nejaky material kde je vysvetlene postupne odvodenie normalneho rozdelenia? vsade som nasiel len definiciu uz samotneho normalneho rozdelenia ale chcel by som vidiet ako sa da dopracovat postupnymi krokmi ku zadefinovaniu normalneho rozdelenia. Vopred vdaka.
Offline
#3 07. 04. 2020 11:06
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: normalne rozdelenie
proste nejaky postup kde sa uvidi ako k tomu normalnemu rozdeleniu prideme .. nejak to muselo vzniknut ale vsade je uz len samotna definicia ..
Offline
#4 07. 04. 2020 11:33
Re: normalne rozdelenie
↑ statistika_je_naj:
Kolega Stýv bude mít jako ostřílený statistik možná lepší nasměrování, ale já bych se asi podíval na nějaký důkaz centrální limitní věty. To by mohlo být to, co hledáš.
Offline
#5 07. 04. 2020 11:33
Re: normalne rozdelenie
Zkus is přečíst https://en.wikipedia.org/wiki/Normal_di … on#History
Offline
#6 07. 04. 2020 11:45
Re: normalne rozdelenie
↑ statistika_je_naj:
Tam to 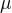 a
a  je jen posouvání, resp. roztahování grafu tak, aby to vyhovovalo skutečné střední hodnotě a rozptylu. To
je jen posouvání, resp. roztahování grafu tak, aby to vyhovovalo skutečné střední hodnotě a rozptylu. To 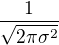 je tam tam proto, aby obsah plochy pod grafem byla jednička (100 % pravděpodobnost).
je tam tam proto, aby obsah plochy pod grafem byla jednička (100 % pravděpodobnost).
No a proč ten základní předpis je zrovna  , ti musí vysvětlit někdo jinej :-)
, ti musí vysvětlit někdo jinej :-)
Offline
#7 07. 04. 2020 12:30
Re: normalne rozdelenie
↑ statistika_je_naj: Because they occur so frequently, there is an unfortunate tendency to invoke normal distributions in situations where they may not be applicable. As Lippmann stated, "Everybody believes in the exponential law of errors: the experimenters, because they think it can be proved by mathematics; and the mathematicians, because they believe it has been established by observation" (Whittaker and Robinson 1967, p. 179).
Offline
#8 07. 04. 2020 15:10
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: normalne rozdelenie
ja chcem to normalne rozdelenie pochopit uplne do zakladov .. statistika je taka oblast matematiky, ktoru pouziva hocikto ale len malo kto jej rozumie do hlbky ..
Offline
#9 07. 04. 2020 16:03
Re: normalne rozdelenie
Ale Gaussovo rozložení nelze nijak odvodit...v principu je to rozložení jako každé jiné...
No, lze ukázat, že pokud máme nějakou náhodnou veličinu ... třeba poslouponost hodnot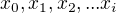
které podléhají jakémukoliv (asi s nějakými omezeními) rozložení, tak když vytvoříme novou posloupnost tím,že sečteme vždy N po sobě jdoucích xi, tak ta nová posloupnost má skoro to Gaussovo rozložení (když je N dostatečně velké).
Takže tím je Gaussovo rozložení výjimečné, ale jinak ... to bude nejspíš jak zmínil ↑ vlado_bb: - matematikové věří, že je lze dokázat experimentálně a fyzikové, že je lze dokázat teoreticky ... a proto to všichni pořád na všechnou používají.
Já bych možná ještě doplni - že všichni to používají, protože se jim už nehce studovat a řešit něco dalšího...
Ze skušenosti znám řadu věcí, které Gaussovo rozložení rozhodně nesplňují. Třeba věková struktura obyvatel ČR.
Offline
#10 07. 04. 2020 16:05
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: normalne rozdelenie
MichalAld napsal(a):
Ale Gaussovo rozložení nelze nijak odvodit...v principu je to rozložení jako každé jiné...
No, lze ukázat, že pokud máme nějakou náhodnou veličinu ... třeba poslouponost hodnot
které podléhají jakémukoliv (asi s nějakými omezeními) rozložení, tak když vytvoříme novou posloupnost tím,že sečteme vždy N po sobě jdoucích xi, tak ta nová posloupnost má skoro to Gaussovo rozložení (když je N dostatečně velké).
toto by ma zaujimalo, ako sa to da ukazat? :)
Offline
#11 07. 04. 2020 16:23
Re: normalne rozdelenie
↑ statistika_je_naj:
Znova opakuju - podívej se na centrální limitní větu. Píšeš, jak chceš pravděpodobnosti a statistice rozumět, tak více čti a méně piš.
Offline
#12 07. 04. 2020 16:39
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: normalne rozdelenie
tu vetu som nasiel ale neviem najst dokaz po cesky alebo slovensky
Offline
#13 07. 04. 2020 17:54
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: normalne rozdelenie
↑ statistika_je_naj:
Nečakaj že niečo nájdeš...skôr by som sa na tvojom mieste pozeral po zahraničných zdrojoch, anglických alebo ruských (keby tu bol kolega vanok ten by ťa s veľkou pravdepodobnosťou odkázal na francúzske).
Offline
#15 08. 04. 2020 08:03
Re: normalne rozdelenie
statistika_je_naj napsal(a):
tu vetu som nasiel ale neviem najst dokaz po cesky alebo slovensky
Pokud to musí být česky, důkaz CLV najdeš například v těchto skriptech (oddíl 6.5). Ale jak už ti bylo naznačeno, bez angličtiny budeš mít stejně dřív nebo později problém.
Offline