Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2020 15:34
Invariantni prostory
Zdravím,
těžko se mi žvýká následující věta, především jeho důkaz:
kde .
.
Důkaz:
Dost by mi pomohl nějaký příklad. Mám slabé základy z lingebry a tak pravděpodobně technicky rozepsaná první rást důkazu bude špatně:
Offline
#2 16. 04. 2020 18:59
Re: Invariantni prostory
ahoj ↑ anddry97:
mozno pomoze trocha vizualizacie
zoberme si transformaciu 
s maticou 
transformácia skosí vertikálny rozmer, pozri obrázok (ten je zhruba)
mozes skusit prehnat maticou vektory standardnej bazy ako sa zobrazia, ukaze sa ze
podpriestor
![kopírovat do textarea $L([1,0])$](/mathtex/b4/b4618ae6be049ac55d91104eace18ab9.gif) sa "nepohne transformaciou", t.j.
sa "nepohne transformaciou", t.j. ![kopírovat do textarea $\varphi (L([1,0]))\subset L([1,0])$](/mathtex/46/468b5222854f5fd224ee05b0c2a8b7bb.gif)
ale pre
![kopírovat do textarea $L([0,1])$](/mathtex/3b/3bf44b5599619a201a2641d3fc953223.gif) uz to neplati (obraz na obrazku zvyrazneny cervenou)
uz to neplati (obraz na obrazku zvyrazneny cervenou)mozes si pre jednoduchost takto predstavit invariant dimenzie

potom napriklad rotacia priestoru
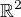 o 60 stupnov jednorozmerny invariantny priestor nema
o 60 stupnov jednorozmerny invariantny priestor nemamatica transformacie

nebude mat v ziadnej baze priestoru polorozpadnuty tvar
Offline




