Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 04. 2020 14:10
#5 23. 04. 2020 15:41
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: Matematická analýza
↑ Pomeranc:
Ahoj, to nejde vyřešit, je tam neznámá funkce y a ty integrály jsou podmínka, kterou musí ta funkce splňovat.
"Máte úhel beta." "No to nemám."
Offline
#10 24. 04. 2020 19:11
#11 24. 04. 2020 19:20 — Editoval MichalAld (24. 04. 2020 19:29)
Re: Matematická analýza
Přesněji tedy, když vezmu třeba ten první příklad, tak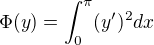



tak by se měl hledat extrém funkcionálu 
Takže 
Provedeme příslušné derivace a dosadíme do toho vztahu
tím dostaneme diferenciální rovnici a její řešení (splňující též okrajové podmínky) by mělo realizovat extrém toho prvního funkcionálu i požadovanou vazbu.
Nebo se to tak nedělá ?
Offline
#12 24. 04. 2020 19:27
Re: Matematická analýza
Jestli dobře počítám, tak by to mělo vyjít
tedy
Dále podle mě, abychom dokázali splnit ty okrajové podmínky, musí být lambda záporné (aby tam bylo v rovnici plus, pak to bude dávat jako řešení siny a cosiny ... a z nich už lze vybrat takové, co nám okrajové podmínky splní.
Ale vše je úplně bez záruky, spíš bych byl rád, kdyby mi někdo kdo tomu trochu rozumí potvrdil nebo rozporoval ten postup...
Offline


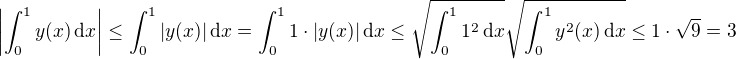
 tak plati
tak plati
 ?
?
