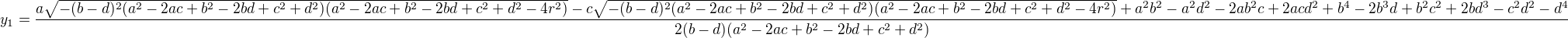Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 05. 2020 21:43
Analytická geometrie - dvě řešení jedné úlohy se liší
Hledal jsem v rovině střed [x,y] kružnice o poloměru r, která prochází body [a,b] a [c,d].
Podle úvahy, že ten hledaný bod [x,y] bude ležet na průsečíku dvou kružnic o poloměru r se středy [a,b] a [c,d]
(obr. 1) jsem vzal rovnice dvou kružnic
(x-a)^2+(y-b)^2=r^2
(x-c)^2+(y-d)^2=r^2
a zadal do WolframAlpha jako solve (x-a)^2+(y-b)^2=r^2,(x-c)^2+(y-d)^2=r^2 for x,y
Ten mi vrátil něco takového (1) (pro první ze dvou možných řešení):
x1 = (a^3 - sqrt(-(b - d)^2 (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2) (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2 - 4 r^2)) - a^2 c + a b^2 - 2 a b d - a c^2 + a d^2 + b^2 c - 2 b c d + c^3 + c d^2)/(2 (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2))
y1 = (a sqrt(-(b - d)^2 (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2) (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2 - 4 r^2)) - c sqrt(-(b - d)^2 (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2) (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2 - 4 r^2)) + a^2 b^2 - a^2 d^2 - 2 a b^2 c + 2 a c d^2 + b^4 - 2 b^3 d + b^2 c^2 + 2 b d^3 - c^2 d^2 - d^4)/(2 (b - d) (a^2 - 2 a c + b^2 - 2 b d + c^2 + d^2))
ale připojil podmínku, že b ≠ d.
Výpočet má být v Excelu a v praxi občas bude b = d, proto se mi to nechtělo nějak obcházet, tak jsem zkusil jiný
postup, našel jsem si střed úsečky [a,b][c,d] = [(a+c)/2,(b+d)/2], z něj vedl kolmou úsečku o délce kterou
jsem určil Pythagorovou větou (obr.2) a vyšlo mi (2) (zase jen pro první řešení):
x1 = ((b-d)*SQRT(r^2-((d-b)^2+(c-a)^2)/4))/SQRT((d-b)^2+(c-a)^2)+(c-a)/2+a
y1 = ((c-a)*SQRT(r^2-((d-b)^2+(c-a)^2)/4))/SQRT((d-b)^2+(c-a)^2)+(d-b)/2+b
Tohle už funguje i pro b = d, takže úkol je tímto splněn. Mně to ale přesto vrtá hlavou, v obou případech počítám
stejné body [x,y], tak proč v jednom případě ta podmínka b ≠ d ? Může za to jenom moje nešikovnost, že neumím
řešení (1) převést na (2) nebo jsem řešil dvě různé úlohy? Může mi prosím někdo napovědět?
Děkuji.
Offline
#4 15. 05. 2020 12:49
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Analytická geometrie - dvě řešení jedné úlohy se liší
Wolfram je známy tým, že výsledky dosť často generuje vo všeobecnej, nezjednodušenej forme, pretože on nedokáže posúdiť, že riešiš planimetrickú úlohu a teda niektoré členy v tom predpise je možné navzájom odčítať, vykrátiť, vyňať a pod.
To čo u člena  naznačil kolega ↑ medvidek: sa určite bude dať spraviť aj s členom
naznačil kolega ↑ medvidek: sa určite bude dať spraviť aj s členom  , pričom po úpravách by si sa mal vedieť dopracovať ku svojim podstatne jednoduchším zápisom, ktoré si našiel pomocou toho druhého postupu.
, pričom po úpravách by si sa mal vedieť dopracovať ku svojim podstatne jednoduchším zápisom, ktoré si našiel pomocou toho druhého postupu.
Offline
#6 15. 05. 2020 18:17
Re: Analytická geometrie - dvě řešení jedné úlohy se liší
↑ Aleš13:
Zkus si s tím vyhrát tak, aby ti vyšlo následující:
Offline


 a vykrátit. Tím se odstraní podmínka
a vykrátit. Tím se odstraní podmínka 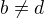 .
.