Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 10. 2009 10:32 — Editoval faktorial (03. 10. 2009 10:33)
sutava rovnic
ahojte,
tu je znenie ulohy:
valec s vyskou 4 cm s polomerom podstavy 5 cm premente na rotacny kuzel s rovnakym povrchom a objemom.
takze mam objem kuzela: V=1/3*pi*r*r*v dalej mam povrch kuzela S=pi*r*r+pi*r*s . to s mozem nahradit s=sqrt(v*v+r*r) toto dosadim do vzorca kuzela namiesto s a uz budem mat len dve nezname. dalej kedze r a v povrchu kuzela a objemu kuzela su rovnake tak tieto dve vzorce pouzijem v sustave dvoch rovnic. lenze ked dosadim toto s=sqrt(v*v+r*r) do S kuzela dostanem : S=pi*r*r+pi*r*sqrt(v*v+r*r), uz je to velmi komplikovane na sustavu rovnic pre mna. lebo ked si vyjadrim z tohto V=1/3*pi*r*r*v v, to bude v=V/(1/3*pi*r*r) a ked toto dosadim do povrchu kuzela dostanem toto : S=pi*r*r+pi*r*sqrt(sqr(V/(1/3*pi*r*r))+r*r) a uz je to komplikovane pre mna toto vypocitat.
a S valca je S=282.6 a V=314, to aby ste nemuseli toto pocitat, toto staci len dosadit a nejak to vypocitat, cize vysledna rovnica je potom:
282.6=pi*r*r+pi*r*sqrt(sqr(314/(1/3*pi*r*r))+r*r)
prosim niekto kto by to vedel nech to prepocita
Offline
#2 04. 10. 2009 09:33 — Editoval jelena (04. 10. 2009 09:35)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: sutava rovnic
↑ faktorial:
Zdravím,
asi se to spatne cetlo nebo se nechtelo vzpisovat, proto nekdo neodpovida, pravdepodobne. Ponechavala jsem v zapisu V, S  a po vykraceni
a po vykraceni  mam>
mam>
z objemu kuzele 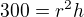 , z obsahu povrchu
, z obsahu povrchu 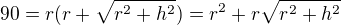 .
.
h - vyska kuzele, r - polomer podstavy kuzele. Veskere upravy provadim za predpokladu, ze rozmery jsou hodnoty kladne.
z 1. rovnice vyjadrim 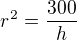 a dosadim do 2. rovnice
a dosadim do 2. rovnice 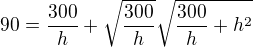 .
.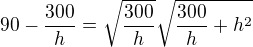 upravim a umocnim levou, pravou stranu
upravim a umocnim levou, pravou stranu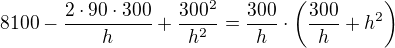
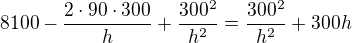 , trochu uprav
, trochu uprav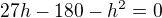 . k reseni je kvadraticka rovnice
. k reseni je kvadraticka rovnice 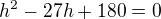
Snad v upravach nemam nejakou chybu a stroj to dokoncil takto
Je vsechno srozumitelne?
Offline
#3 05. 10. 2009 15:03 — Editoval faktorial (05. 10. 2009 15:32)
Re: sutava rovnic
premna je to prilis komplikovane, aj ked sa to da takto vypocitat, ale nepoznas nejake jednoduchsie riesenie?
mne vysla takato kvadraticka rovnica (ja som pouzil iny postup riesenia):
79524*r*r-564*pi*r*r*r*r-887364=0
je to dobre? a vysliel jeden vysledok okolo 3.3 a druhy koren zaporne co je zle.
Offline
#4 05. 10. 2009 16:11 — Editoval Chrpa (06. 10. 2009 07:48)
Re: sutava rovnic
↑ faktorial:
To řešení co navrhla ↑ jelena: je podle mě jednodušší, než to tvoje.
Vždyť to vychází pěkně: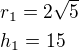 nebo
nebo 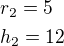
Co bys ještě více chtěl?
Postup od ↑ jelena: je zcela srozumitelný a jednoduchý.
PS
Ta tvá rovnice (pokud jsem ji dobře odečetl) tak vychází: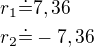 což jak uznáš, není dobře.
což jak uznáš, není dobře.
Obrázek:
http://forum.matweb.cz/upload/1254808066-avak1.JPG
Offline