Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Základy lineární regrese - odhad koeficientu s nejmensim rozptylem
#1 08. 06. 2020 21:05 — Editoval Andrew123 (08. 06. 2020 21:06)
Základy lineární regrese - odhad koeficientu s nejmensim rozptylem
Ahoj, počítám si příklady ze sbírky aplikované statistiky (skripta VŠCHT) a s jedním příkladem si moc nevím rady. Jedná se o kapitolu Základy regresní analýzy. Text příkladu je následujici:
Zadání:
Předpokládejme, že prodloužení pružiny  závisí na zatěžovací síle
závisí na zatěžovací síle  v rozmezí
v rozmezí  lineárně:
lineárně: 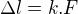 . Aby se při odhadu konstanty
. Aby se při odhadu konstanty  omezil vliv náhodných chyb měření
omezil vliv náhodných chyb měření 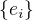 , o kterých se predpokládá, že jsou to nezávislé náhodné veličiny, splňujcí rovnice
, o kterých se predpokládá, že jsou to nezávislé náhodné veličiny, splňujcí rovnice 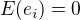 ,
, 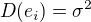 , bylo rozhodnuto měření desetkrát opakovat. Získané hodnoty
, bylo rozhodnuto měření desetkrát opakovat. Získané hodnoty 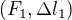 , ...,
, ..., 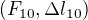 splňují vztahy
splňují vztahy 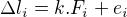 ,
, 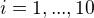 . Jak volit hodnoty
. Jak volit hodnoty 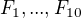
 , aby odhad
, aby odhad 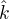 , získaný metodou nejmenších čtverců, byl nejlepší, tj. měl nejmenší rozptyl? Jaký bude mít při optimální volbě
, získaný metodou nejmenších čtverců, byl nejlepší, tj. měl nejmenší rozptyl? Jaký bude mít při optimální volbě 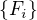 odhad
odhad 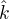 tvar?
tvar?
Správný výsledek ve sbírce je uveden: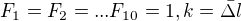 .
.
Můj neúplný začátek postupu:
Počítám se vztahem 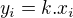 , kde
, kde 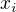 odpovídá
odpovídá 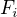 a
a  odpovídá
odpovídá 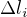 . Vztah pro rozptyl jsem si našel, že je nasledující:
. Vztah pro rozptyl jsem si našel, že je nasledující: 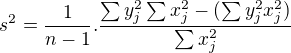 . Předpokládám, že je mým cílem minimalizovat tuto funkci
. Předpokládám, že je mým cílem minimalizovat tuto funkci 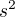 . Je to tak? Jedná se však o funkci s 10 proměnnými, což není jednoduché. Očekávám, že by to mělo jít vyřešit nějak jednodušeji a nějakým trikem. Nejedná se o žádný příklad s hvězdičkou či tak něco.
. Je to tak? Jedná se však o funkci s 10 proměnnými, což není jednoduché. Očekávám, že by to mělo jít vyřešit nějak jednodušeji a nějakým trikem. Nejedná se o žádný příklad s hvězdičkou či tak něco.
Může mi někdo prosim poradit, jak dojít k výsledku?
Dekuji, Andrew
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Základy lineární regrese - odhad koeficientu s nejmensim rozptylem