Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Jeden specialny determinant
#1 18. 07. 2020 20:47 — Editoval vanok (23. 07. 2020 15:48)
Jeden specialny determinant
Pozdravujem,
Tu v #46 som popisal ako sa da najst jeden specialny determinant.
Teraz tu ukazem ako nast trocha vseobecnejsi determinant.
Urcite  , kde
, kde  .
.
Na jeho urcenie mozme pouzit tuto myslienku:
Pridajme ku kazdemu prvku z 
 a oznacme tento novy determinant
a oznacme tento novy determinant 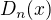 .
.
Poznamka: predpokladajme, ze vsetki konstanty v tomto vlakne su v lubolnom komutativnom telese.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 23. 07. 2020 14:33 — Editoval vanok (23. 07. 2020 15:40)
Re: Jeden specialny determinant
Teraz porozmyslajme trochu o 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 23. 07. 2020 15:35
Re: Jeden specialny determinant
Ukazme, ze mame  , kde
, kde 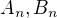 su konstaty.
su konstaty.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 24. 07. 2020 23:04 — Editoval vanok (25. 07. 2020 09:15)
Re: Jeden specialny determinant
Teraz odpocitajme od prvych n-1 stlpcov posledny a rozvinieme podla posledneho stlpca, dostaneme #3.
Tiez vidime, ze 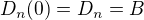
Lahko dostaneme 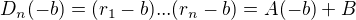 .
.
Podobne urcime 
Posledne dve rovnosti, nam umoznuju urcit 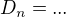 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 26. 07. 2020 12:17 — Editoval vanok (26. 07. 2020 12:50)
Re: Jeden specialny determinant
[re]p611768|vanok[/,
Kontrola .
Iste ste nasli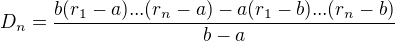
(Vsak kazdy vie riesit linearny system 2x2 ).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 26. 07. 2020 12:37
Re: Jeden specialny determinant
Co sa tyka pripadu 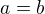 to necham to na vas.
to necham to na vas.
Poznamka.
V pripade realneho determinantu, dokaz je mimoriadne jednoduchy.
No ale aj vseobecny pripad je velmi zaujimavy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Jeden specialny determinant
