Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 08. 2020 11:23 — Editoval liamlim_2 (16. 08. 2020 11:55)
Velká Fermatova věta - opraveno
[Opravená verze předchozího příspěvku, který jsem bohužel nemohl editovat]
Prosím mohl by se někdo podívat, jestli v následujícím nemám nějakou chybu? Děkuji :) Všechno by to měly být jen čistě středoškolské operace, žádná vysoká matematika.
Nechť  ,
,  a
a  jsou po dvou nesoudělná čísla a
jsou po dvou nesoudělná čísla a 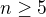 je prvočíslo. Dále nechť
je prvočíslo. Dále nechť 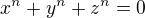 .
.
Úpravami dostaneme:
(1) 
(2) 
Nyní uveďme pomocné tvrzení. Pro libovolná nesoudělná  ,
,  a prvočíselné
a prvočíselné 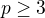 platí, že každý dělitel čísla
platí, že každý dělitel čísla  je buď
je buď  nebo je tvaru
nebo je tvaru 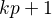 pro nějaké nenulové celočíselné
pro nějaké nenulové celočíselné  .
.
Důkaz není tak obtížný a na požádání ho uvedu. Tady by ale zbytečně zabíral místo a činil celý text méně přehledným.
Nyní definujme pro celočíselné  hodnotu
hodnotu  jako největší dělitel čísla
jako největší dělitel čísla  takový, že
takový, že  nedělí
nedělí  a současně žádný z dělitelů čísla
a současně žádný z dělitelů čísla  není ani
není ani  ani tvaru
ani tvaru  pro celočíselné
pro celočíselné  .
.
S využitím (1) a (2) spolu s definicí  dostaneme
dostaneme
- 
- 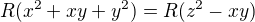
Díky symetrii v  ,
,  a
a  potom můžeme definovat
potom můžeme definovat
(3) 
Z definice  víme, že
víme, že  dělí
dělí  a současně
a současně  dělí
dělí  , dělí i tedy jejich rozdíl, což je
, dělí i tedy jejich rozdíl, což je 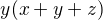 . Vzhledem k nesoudělnosti
. Vzhledem k nesoudělnosti  ,
,  a
a  dostaneme:
dostaneme:
(4)  dělí
dělí 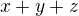 neboli
neboli  dělí
dělí 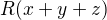
Protože  dělí
dělí 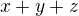 a současně
a současně  dělí
dělí  , musí dělit i pokud dosadíme
, musí dělit i pokud dosadíme 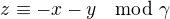 do kongruence
do kongruence  neboli
neboli 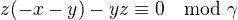 neboli
neboli
(5)  dělí
dělí  neboli
neboli  dělí
dělí  .
.
Nyní definujme 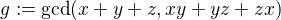 . Pak z (4) a (5) okamžitě plyne
. Pak z (4) a (5) okamžitě plyne
(6)  dělí
dělí  neboli
neboli  dělí
dělí 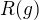 .
.
Protože  je největší společný dělitel
je největší společný dělitel 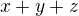 a
a  , musí
, musí  dělit též pokud dosadíme
dělit též pokud dosadíme 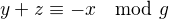 do
do  , čímž dostaneme, že
, čímž dostaneme, že  dělí
dělí 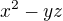 . Proto
. Proto 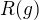 dělí
dělí  , přitom ale
, přitom ale  dělí
dělí 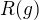 , proto
, proto
(7) 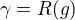
Další krok v mém "důkazu" je dokázat indukcí, že pro libovolné přirozené  máme:
máme:
(8) 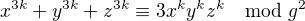
(9) 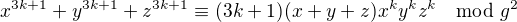
(10) 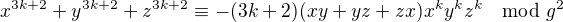
kde 
Ten důkaz je opravdu přímočará indukce s tím, že pokaždé využijeme toho, že 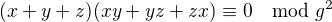 ,
,  a
a  .
.
Offline
#2 16. 08. 2020 18:07 — Editoval check_drummer (16. 08. 2020 18:09)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
Prosím o uvedení důkazu:
liamlim_2 napsal(a):
Nyní uveďme pomocné tvrzení. Pro libovolná nesoudělná
,
a prvočíselné
platí, že každý dělitel čísla
je buď
nebo je tvaru
pro nějaké nenulové celočíselné
.
Proč platí:
liamlim_2 napsal(a):
(5)
dělí
neboli
dělí
.
?
Stejný dotaz pro bod (4).
Stále jsi neuvedl, že v některých případech je R(a) dodefinováno jako 1.
"Máte úhel beta." "No to nemám."
Offline
#3 16. 08. 2020 21:46
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
Rád bych to zase opravil, protože jsem skutečně předpoklad o R(a) dodefinovaném jako 1 neuvedl. Já můžu editovat pouze mé odpovědi, ale nikoliv hlavní příspěvek.
Jinak ohledně  dělí
dělí  neboli
neboli  dělí
dělí  . Hodnota
. Hodnota  je definovaná jako
je definovaná jako 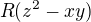 , tedy všechny dělitele
, tedy všechny dělitele  nejsou ani
nejsou ani  ani tvaru
ani tvaru  . Proto pokud z
. Proto pokud z  odděláme všechny dělitele tvaru
odděláme všechny dělitele tvaru  nebo
nebo  , tak pořád
, tak pořád  dělí výsledné číslo, protože VŠECHNY dělitelé
dělí výsledné číslo, protože VŠECHNY dělitelé  jsou jiného tvaru než
jsou jiného tvaru než  nebo
nebo  . No a funkce
. No a funkce  nám udělá přesně to, co chceme. Odfiltruje nám všechny "špatné" dělitele, které jsou tvaru
nám udělá přesně to, co chceme. Odfiltruje nám všechny "špatné" dělitele, které jsou tvaru  nebo
nebo 
Offline
#4 16. 08. 2020 22:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Velká Fermatova věta - opraveno
Zdravím,
↑ check_drummer:, ↑ liamlim_2:
už si vybavuji, v čem je zádrhel - v nastavení pravidla pro editaci 1. příspěvku
Pavel Brožek v roce 2012 napsal(a):
Pokud nikdo neodpověděl, tak je editace možná kdykoliv. Pokud někdo odpověděl, tak jen do dvou hodin od založení tématu.
↑ liamlim_2: prosím o část, kterou mám zeditovat (nejjednodušší do dalšího příspěvku vlož, prosím, celý text prvního s barevným označením, co mám editovat). Na druhou stranu - pokud jde jen o vývoj diskuse, tak se dá předpokládat, že ne všechno bude rovnou v 1. příspěvku, ale že vyplyne z diskuse. Děkuji za upřesnění, co s editem.
Offline
#5 17. 08. 2020 10:08 — Editoval liamlim_2 (17. 08. 2020 10:27)
Re: Velká Fermatova věta - opraveno
Důkaz toho pomocného tvrzení je jednoduchý. Nechť  je libovolný prvočíselný dělitel čísla
je libovolný prvočíselný dělitel čísla 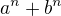 , který není ani tvaru
, který není ani tvaru  . Pak
. Pak  je též dělitel čísla
je též dělitel čísla 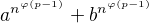 , kde
, kde  je eulerova funkce. Protože
je eulerova funkce. Protože  není tvaru
není tvaru  , můžeme psát
, můžeme psát 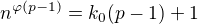 . Po dosazení máme, že
. Po dosazení máme, že  dělí
dělí  neboli
neboli  dělí
dělí 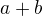 . Už odsud plyne hlavní část tvrzení, totiž že libovolný prvočíselný dělitel čísla
. Už odsud plyne hlavní část tvrzení, totiž že libovolný prvočíselný dělitel čísla 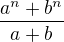 , který není tvaru
, který není tvaru  dělí
dělí 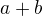 .
.
Pro dokončení důkazu stačí ukázat, že 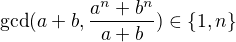 . To se dokáže triviálně ze vztahu
. To se dokáže triviálně ze vztahu 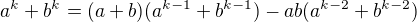 platného pro libovolné
platného pro libovolné  s využitím matematické indukce
s využitím matematické indukce
Offline
#6 17. 08. 2020 13:50
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
Toto plyne z čeho?
liamlim_2 napsal(a):
Nechť
je libovolný prvočíselný dělitel čísla
, který není ani tvaru
. Pak

je též dělitel čísla, kde
je eulerova funkce.
"Máte úhel beta." "No to nemám."
Offline
#7 17. 08. 2020 14:11
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
↑ jelena:
Ahoj, pokud se to týká jen prvního příspěvku, tak pro účely tohoto příspěvku navrhuju první příspěvek založit jako fejk a hlvní téma dat do druhého, a ten už pak bude moci autor neomezeně editovat. :-)
"Máte úhel beta." "No to nemám."
Offline
#8 17. 08. 2020 14:19 — Editoval liamlim_2 (17. 08. 2020 14:19)
Re: Velká Fermatova věta - opraveno
↑ check_drummer: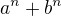 dělí
dělí 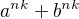 pro každé liché přirozené
pro každé liché přirozené  . Tedy i pro
. Tedy i pro 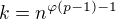 , proto
, proto 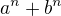 dělí
dělí 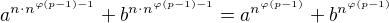 . Protože
. Protože  dělí
dělí 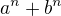 a
a 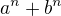 je dělitel čísla
je dělitel čísla 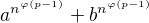 , tak
, tak  dělí
dělí 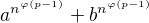
Offline
#9 17. 08. 2020 14:29
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
A toto plyne z čeho?
liamlim_2 napsal(a):
dělí
pro každé liché přirozené
.
"Máte úhel beta." "No to nemám."
Offline
#10 17. 08. 2020 14:33 — Editoval liamlim_2 (17. 08. 2020 14:39)
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
Toto plyne z toho, že  , do čehož dosadíme
, do čehož dosadíme 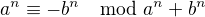 , což pro liché
, což pro liché  dá
dá 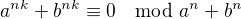
Obecně platí pro liché  vztah
vztah 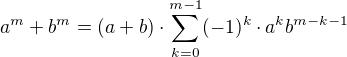 , což jde snadno dokázat indukcí přes
, což jde snadno dokázat indukcí přes  . Dosazením
. Dosazením 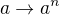 ,
,  dostaneme taky co potřebujeme :)
dostaneme taky co potřebujeme :)
Offline
#11 17. 08. 2020 15:07 — Editoval liamlim_2 (17. 08. 2020 15:20)
Re: Velká Fermatova věta - opraveno
[Nejnovější verze mého "důkazu". Dost zjednodušená]
Nechť  ,
,  a
a  jsou po dvou nesoudělná čísla a
jsou po dvou nesoudělná čísla a 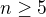 je prvočíslo. Dále nechť
je prvočíslo. Dále nechť 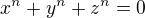 .
.
Úpravami dostaneme:
(1) 
(2) 
Nyní uveďme pomocné tvrzení. Pro libovolná nesoudělná  ,
,  a prvočíselné
a prvočíselné 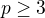 platí, že každý dělitel čísla
platí, že každý dělitel čísla  je buď
je buď  nebo je tvaru
nebo je tvaru 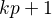 pro nějaké nenulové celočíselné
pro nějaké nenulové celočíselné  .
.
[důkaz jsem již uvedl dříve]
Nyní definujme pro celočíselné  hodnotu
hodnotu  jako největší dělitel čísla
jako největší dělitel čísla  takový, že
takový, že  nedělí
nedělí  a současně žádný z dělitelů čísla
a současně žádný z dělitelů čísla  není ani
není ani  ani tvaru
ani tvaru  pro nějaké nenulové celočíselné
pro nějaké nenulové celočíselné  . Pokud takové číslo neexistuje, pak dodefinujeme
. Pokud takové číslo neexistuje, pak dodefinujeme  .
.
S využitím (1) a (2) spolu s definicí  dostaneme
dostaneme
- 
- 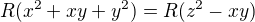
Díky symetrii v  ,
,  a
a  potom můžeme definovat
potom můžeme definovat
(3) 
4.a) Jestliže  dělí
dělí  , pak
, pak  dělí
dělí 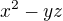 a
a  dělí
dělí 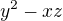 .
.
4.b) Jestliže  dělí
dělí  , pak
, pak  dělí
dělí 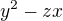 a
a  dělí
dělí  .
.
4.c) Jestliže  dělí
dělí  , pak
, pak  dělí
dělí  a
a  dělí
dělí 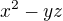 .
.
Důkaz:
Jestliže  dělí
dělí  , tak dělí i
, tak dělí i 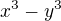 , neboli
, neboli 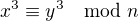 . Proto
. Proto  . Víme, že
. Víme, že  nedělí
nedělí 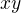 , neboť
, neboť  ,
,  a
a  jsou nesoudělná a
jsou nesoudělná a  dělí
dělí  , proto by
, proto by  jinak muselo dělit jak
jinak muselo dělit jak  tak
tak  . Proto buď
. Proto buď  dělí jak
dělí jak 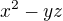 tak
tak 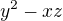 a jsme hotovi, nebo nedělí ani
a jsme hotovi, nebo nedělí ani 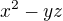 ani
ani 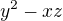 . V takovém případě ale
. V takovém případě ale  , což plyne z toho, že
, což plyne z toho, že  . V takovém případě ale nutně
. V takovém případě ale nutně 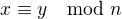 . Po dosazení této kongruence do
. Po dosazení této kongruence do 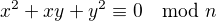 dostaneme, že
dostaneme, že  dělí
dělí 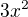 a současně
a současně  dělí
dělí  , tedy
, tedy  dělí 3, což není možné, neboť
dělí 3, což není možné, neboť 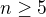 , proto jsme došli ke sporu a jsme hotovi.
, proto jsme došli ke sporu a jsme hotovi.
Další dvě implikace plynou ze symetrie
5.a) Jestliže  dělí
dělí 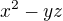 , pak
, pak  dělí
dělí 
5.b) Jestliže  dělí
dělí 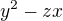 , pak
, pak  dělí
dělí 
5.c) Jestliže  dělí
dělí  , pak
, pak  dělí
dělí 
Důkaz:
Využijeme 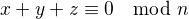 plynoucího z
plynoucího z  , což po dosazení dává
, což po dosazení dává 
(4) a (5) dávají dohromady
(6) Jestliže  dělí libovolné z čísel
dělí libovolné z čísel 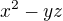 ,
, 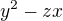 ,
,  ,
,  ,
,  ,
,  , pak dělí i všechny ostatní.
, pak dělí i všechny ostatní.
Offline
#12 17. 08. 2020 17:14
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
liamlim_2 napsal(a):
...můžeme psát
.
Jak to?
liamlim_2 napsal(a):
... neboli
dělí
.
Jak to?
"Máte úhel beta." "No to nemám."
Offline
#13 17. 08. 2020 17:34
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
To je skutečně jenom Eulerova věta a poté Malá Fermatova věta, nic z toho jsem nevymyslel já, jenom jsem použil tyto dva nástroje.
Offline
#14 17. 08. 2020 19:59
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
↑ liamlim_2:
Abys mohl použít Eulerovu větu, tak musí platit nsd(n,p-1)=1, že? To plyne z čeho?
"Máte úhel beta." "No to nemám."
Offline
#15 17. 08. 2020 20:17 — Editoval liamlim_2 (17. 08. 2020 20:19)
Re: Velká Fermatova věta - opraveno
↑ check_drummer: To plyne z "prvočíselného dělitele  , který není tvaru
, který není tvaru  ."
."
Já se snažím dokázat, že 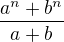 má POUZE dělitele tvaru
má POUZE dělitele tvaru  nebo
nebo  . Proto mě zajímají jen ty prvočíselné dělitele
. Proto mě zajímají jen ty prvočíselné dělitele 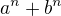 , které nejsou tvaru
, které nejsou tvaru  . Pokud
. Pokud  není tvaru
není tvaru  abych ukázal, že všechny takové dělitele musí dělit i
abych ukázal, že všechny takové dělitele musí dělit i 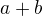 . Pokud ale
. Pokud ale  není tvaru
není tvaru  , pak
, pak 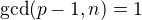 , což je přesně to, co potřebuji
, což je přesně to, co potřebuji
Offline
#16 17. 08. 2020 20:46
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
↑ liamlim_2:
Asi je potřeba tiu Eulerovu větu a Malou Fermatovu rozepsat postupně - nejprve na  a pak na
a pak na  , protože obě věty se netýkají součtu mocnin, ale jen jediné mocniny. Možná že díky tomu zjistíme, že nepůjde volit jedno
, protože obě věty se netýkají součtu mocnin, ale jen jediné mocniny. Možná že díky tomu zjistíme, že nepůjde volit jedno  , ale že budou muset být pro a,b jiné, ale uvidíme.
, ale že budou muset být pro a,b jiné, ale uvidíme.
"Máte úhel beta." "No to nemám."
Offline
#17 17. 08. 2020 23:10
Re: Velká Fermatova věta - opraveno
↑ check_drummer:,
Ta lemma z #15 sa da dokazat aj vdaka bionickej vete.
( uvazuj dva pripady prvocislo n|a+b, a potom, ze n nedeli a+b)
Poznamka: zvysok textu som necital .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 18. 08. 2020 03:24
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
liamlim_2 napsal(a):
Už odsud plyne hlavní část tvrzení, totiž že libovolný prvočíselný dělitel čísla
, který není tvaru
dělí
.
Jak to? Dokázali jsme, že libovolný prvočíselný dělitel čísla 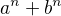 , který není tvaru
, který není tvaru  dělí
dělí 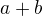 .
.
"Máte úhel beta." "No to nemám."
Offline
#19 18. 08. 2020 03:38
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
liamlim_2 napsal(a):
Pro dokončení důkazu stačí ukázat, že
. To se dokáže triviálně ze vztahu
platného pro libovolné
s využitím matematické indukce
1) Proč to platí?
2) proč to stačí k důkazu toho tvrzení?
"Máte úhel beta." "No to nemám."
Offline
#20 18. 08. 2020 05:28
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
Když libovolný prvočíselný dělitel správného tvaru čísla 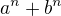 dělí
dělí 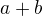 , tak tím spíš libovolný prvočíselný dělitel správného tvaru čísla
, tak tím spíš libovolný prvočíselný dělitel správného tvaru čísla 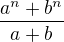 dělí
dělí 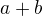 , neboť
, neboť 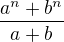 dělí
dělí 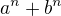
Offline
#21 18. 08. 2020 05:32
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
Ukázali jsme, že libovolný prvočíselný dělitel čísla 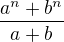 , který není tvaru
, který není tvaru  dělí
dělí 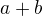 . Proto abychom dokázali, že žádný prvočíselný dělitel, který není tvaru
. Proto abychom dokázali, že žádný prvočíselný dělitel, který není tvaru  , čísla
, čísla 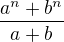 neexistuje, tak nám stačí ukátat, že neexistuje prvočíselný dělitel tvaru
neexistuje, tak nám stačí ukátat, že neexistuje prvočíselný dělitel tvaru  čísla
čísla  , k čemuž nám stačí ukázat
, k čemuž nám stačí ukázat 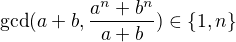 , neboť ani 1 ani
, neboť ani 1 ani  nejsou tvaru
nejsou tvaru  pro nenulové
pro nenulové  .
.
Offline
#22 18. 08. 2020 05:39
Re: Velká Fermatova věta - opraveno
↑ check_drummer:↑ check_drummer:
Protože ze 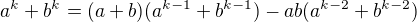 plyne pro liché
plyne pro liché 
vztah 
Není třeba zdůvodňovat jak tento vtah plyne z předchhozího, stačí indukcí dokázat toto tvrzení. Díky tomu dojdeme k faktu, že  dělí
dělí  pro libovolné liché
pro libovolné liché  .
.
Offline
#23 18. 08. 2020 15:28 — Editoval check_drummer (18. 08. 2020 17:01)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
liamlim_2 napsal(a):
plyne pro liché
vztah
Jak to? (A)
liamlim_2 napsal(a):
Díky tomu dojdeme k faktu, že
dělí
pro libovolné liché
.
Jak to (B) a jak to souvisí s dokazovaným (C):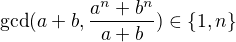
"Máte úhel beta." "No to nemám."
Offline
#24 18. 08. 2020 16:21 — Editoval liamlim_2 (18. 08. 2020 16:23)
Re: Velká Fermatova věta - opraveno
↑ check_drummer:
mně připadá, že říkám pořád dokola to samotné. My jsme ukázali, že libovolný dělitel 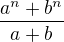 který není tvaru
který není tvaru  dělí
dělí 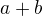 . Tím ale ještě nevíme, jestli takový dělitel vůbec existuje (a chceme ukázat že ne). Proto se podíváme na největší společný dělitel čísel
. Tím ale ještě nevíme, jestli takový dělitel vůbec existuje (a chceme ukázat že ne). Proto se podíváme na největší společný dělitel čísel 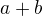 a
a 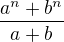 . Pokud žádné z těch čísel nebude tvaru
. Pokud žádné z těch čísel nebude tvaru  , pak tím víme, že neexistuje dělitel čísla
, pak tím víme, že neexistuje dělitel čísla 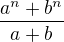 , který není tvaru
, který není tvaru  . Ten by totiž dělil i
. Ten by totiž dělil i 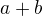 a tedy i
a tedy i  . Tím že ukážeme, že
. Tím že ukážeme, že 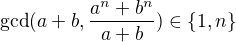 tak tím ukážeme, že jediným kandidátem na to, aby dělilo jak
tak tím ukážeme, že jediným kandidátem na to, aby dělilo jak 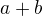 tak
tak 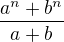 který není tvaru
který není tvaru  je
je  .
.
Offline
#25 18. 08. 2020 16:59 — Editoval check_drummer (18. 08. 2020 17:01)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta - opraveno
↑ liamlim_2:
To ano, ale já se ptám na jiné věci, označím je (A), (B), (C) výše.
"Máte úhel beta." "No to nemám."
Offline
