Matematické Fórum

vanok · 30. 08. 2020 17:21 — Editoval vanok (07. 09. 2020 20:38)

Pozdravujem,
Tu https://forum.matweb.cz/viewtopic.php?id=108939 sa snazime vysletrit stabilne podpriestory pre endomorfismy na vseobecnych vektorovych priestoroch.

V tomto vlakne budeme len komentovat ak treba, vysledky, ktore v dokazame citovanom vlakne.

vanok · 07. 09. 2020 23:12 — Editoval vanok (10. 09. 2020 18:35)

Poznamka.
Je dobre si uvedomit, ze rozne endomorfismy sa redukuju tak, ze priestor na ktorom definovane sa rozlozi na stabilne podpriestory ktorych je priamy sucet, na ktorych dany homomorfismus je jednoduchsi. To tu rozvedieme.
Ale pozor, naviac je zaujimave najt vsetki stabilne podpiestory danevo endomorfismu. ( casto sa o tom vobec ani nehovori).

Tu vyriesime ( podrobne) niekolko cviceni pre rozne endomofismy:

Zacneme z cviceniami diagonizovatelnych, ( vsetki vlastne hodnoty rozlicne) endomorfismov, ktorych povodny priestor E je priama suma vlastnych podpriestorov na ktoryvh povodny endomorismus ma restrikciu homoteciu (= rovnolahlost) na kazdom z nich.

Take je napr. cvicenie v #19 vo vlakne https://forum.matweb.cz/viewtopic.php?id=108939

vanok · 13. 09. 2020 19:32

Co sa tyka diagozivotelnych matic ( endomofismizmov) tu
https://en.wikipedia.org/wiki/Diagonalizable_matrix su dalsie podrobnosti.

vanok · 11. 10. 2020 12:46 — Editoval vanok (11. 10. 2020 12:48)

Tu https://forum.matweb.cz/viewtopic.p … 89#p613289 v #11, #13 a dalsich # ,najdete priklady cviceni, ktore maju suvis z temou tohto vlakna.

vanok · 23. 10. 2020 10:26 — Editoval vanok (23. 10. 2020 11:19)

Len upozornim, ze aj v tomto https://forum.matweb.cz/viewtopic.p … 84#p613284 vlakne najdete uzitocne cvicenia, ktore vam mozu posluzit.

vanok · 31. 10. 2020 14:00 — Editoval vanok (09. 11. 2020 03:43)

Tu https://forum.matweb.cz/viewtopic.p … 44#p614544 som dal v #16 cvicenie, ktore ostalo bez riesenia.
Tak tu sa vratim k podobnemm cviceniu, ale tu bude polozenych viacej otazok (necham vas posudit ako sa tyka stabilnych podpriestorov, diagonalisacii a rozkladu Jordan-Chevalley).
Cvicenie.
Nech $a,b \in \Bbb R$ a $A= \begin{pmatrix} 1 & a & 0\\ 0 & 1 & b\\ 0 & 0 & 2\\ \end{pmatrix}$ .
A.Urcite $a, b$ take aby $A=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix}+ \begin{pmatrix} 0 & a & 0\\ 0 & 0 & b\\ 0 & 0 & 0\\ \end{pmatrix}$
bol rozklad Jordan-Chevalley
B. Polozme teraz $a \neq 0; b=1$
a) Urcite vlastne a charakteristicke podprietory matice $A$ .
b) Najdite rozklad Jordan-Chevalley matice $A$ .

vanok · 01. 11. 2020 14:10 — Editoval vanok (01. 11. 2020 14:12)

Riesenie A z ↑ vanok::
Oznacme $D=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix}$ a $N=\begin{pmatrix} 0 & a & 0\\ 0 & 0 & b\\ 0 & 0 & 0\\ \end{pmatrix}$ .
$D$ je diagonalna, co sa tyka $N$ , mame $N^2= \begin{pmatrix} 0 & 0 & ab\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{pmatrix}$ a $N^3=\begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{pmatrix}$ , a tak $N$ je nilpotentna.

Naviac mame, ze $DN= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix} \begin{pmatrix} 0 & a & 0\\ 0 & 0 & b\\ 0 & 0 & 0\\ \end{pmatrix}= \begin{pmatrix} 0 & a & 0\\ 0 & 0 & b\\ 0 & 0 & 0\\ \end{pmatrix}$
a $ND=\begin{pmatrix} 0 & a & 0\\ 0 & 0 & b\\ 0 & 0 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix} =\begin{pmatrix} 0 & a & 0\\ 0 & 0 & 2b\\ 0 & 0 & 0\\ \end{pmatrix}$ ,
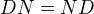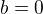a tak $DN=ND$ len a len ak $b=2b$ , cize $b=0$ a $a$ moze byt lubovolne realne cislo.

vanok · 02. 11. 2020 15:08 — Editoval vanok (05. 11. 2020 12:49)

Riesenie otazky B z ↑ vanok:
$A=\begin{pmatrix} 1 & a & 0\\ 0 & 1 & 1\\ 0 & 0 & 2\\ \end{pmatrix}$ .
Riesenie otazky a)
Urcime najprv vlastne podpriestory matice A:
Akoze, A je trojuholnikova , tak 1 je jej dvojnasobna vlastna hodnota a 2 jenodicha vlastna hodnota.
Oznacme $E_1;E_2$ hladane vlastne podpriestory.
$E_1=\{\vec u(x,y,z) \in \Bbb R^3,A\vec u =\vec u \}$ .
Co nam da :
x+ay= x
y+z= y
2z=z
Co je ekvivalentne z
y=z=0 .
Tak podpriestor $E_1$ je generovany vektorom $(1;0;0)$ , ktory je tak dim 1 a je pridruzeny vlastnej hodnote 1.
Co tiez znamena, ze matica A nie je diagonizovatelna .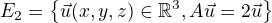

$E_2 =\{\vec u(x,y,z) \in \Bbb R^3,A\vec u =2 \vec u \}$ .
Tu podobne ako pre $E_1$ dokazeme,ze
x=ay
y=z;
co znamena, ze $E_2$ je generovaney vectorom $(a;1;1)$ .
Akoze vlastne hodnota je jednoducha ( = radu 1), tak jej charakteristicky podpriestor je $N_2=E_2$ .
A tu charakteristicky podpriestor pridruzey vlastnej hodnote 1 je 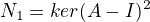$N_1=ker (A-I)^2$
Vypocitajme $(A-I)^2= \begin{pmatrix} 0 & a & 0\\ 0 & 0 & 1\\ 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} 0 & a & 0\\ 0 & 0 & 1\\ 0 & 0 & 1\\ \end{pmatrix}= \begin{pmatrix} 0 & 0 & a\\ 0 & 0 & 1\\ 0 & 0 & 1\\ \end{pmatrix}$
Vidime ze jej jadro je generovane vektorm $\vec e_1(1;0;0);\vec e_2(0;1;0)$ .

vanok · 04. 11. 2020 16:36 — Editoval vanok (06. 11. 2020 02:23)

Riesenie otazky B b) z [re]p614568|vanok[/re,
Tu urcime matice $D$ diagonalizablu a $N$ nipotantu, ktore komutuju a $A=D+N$ .
Nech $\vec e_3(a;1;1)$ je taky vektor, ze v baze je $\vec e_1; \vec e_2; \vec e_3$ matica A pridruzena endomorfismu, ( ktory ju representuje v standardnef baze) sa pise $B=\begin{pmatrix} 1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ \end{pmatrix}=D^*+N^*$ , kde $D^*=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ \end{pmatrix}$ a $N^*=\begin{pmatrix} 0 & a & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{pmatrix}$ .
Je jasne, ze tu mame Jordan-Chevalley rozklad matice $B$ a naviac $A=PBP^{-1}$ , kde $P=\begin{pmatrix} 1 & 0 & a\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{pmatrix}$ a $P^{-1}=\begin{pmatrix} 1 & 0 & -a\\ 0 & 1 & -1\\ 0 & 0 & 1\\ \end{pmatrix}$ ( cf. zmena baz).
Matice $D=PD^*P^{-1}$ a $N=PN^*P^{-1}$ su resp. diagonalizovatelna a nilpotentna a tiez komutuju co nam da hladany rozklad Jordan Chevalley: $A=D+N$ .