Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
#1 22. 09. 2020 22:34
Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
Zdravím Vás,
potřeboval bych objasnit věci ohledně metod Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů. Řeším výbuchy hybridních směsí k tématu mé disertační práce a nyní se nacházím ve stavu, kdy chci ověřit jistý model, který se používá k modelování výbuchů prachů. Článek, ze kterého čerpám však neuvádí přesné postupy a řešení matematického modelu. Jsem spíš fyzikální chemik a tak studium matematického modelování by pro mě byla zbytečná ztráta času, obzvlášť když se jedná pouze o dílčí krok v porvnání s celkovým obsahem disertační práce.
Metodou Runge-Kutta čtvrtého řádu mají být řešeny tyto rovnice:
Metodou Newton-Raphson pak tyto:
Obě metody jsou provázané. Neznámé jsou v jednotlivých rovnicích tyto: rrear, rfront a P.
Výsledkem by měly být grafy, např:
Pro jistotu předpkládám celý článek, rovnice jsou řešeny v části "three-zone model".













Pokud by mi byl někdo schopen pomoct, klidně i za úplatu, bud moc rád. Děkuji. Už jsem opravdu zoufalý.
Offline
#2 23. 09. 2020 01:41 — Editoval laszky (23. 09. 2020 10:01)
Re: Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
Ahoj, tak ja bych rekl, ze:
Pripad 1:
Faze 1a: Zacnes resit ODR (23) pomoci RK4, pricemz postupne pomoci NM aplikovane na (22) dopocitavas 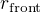 . Jakmile
. Jakmile 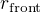 dosahne hodnoty
dosahne hodnoty  jses ve fazi 1b.
jses ve fazi 1b.
Faze 1b: Resis ODR (27) pomoci RK4, pricemz postupne pomoci NM aplikovane na (26) dopocitavas 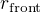 . Nasledne
. Nasledne 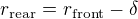 . Jakmile
. Jakmile 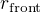 dosahne hodnoty
dosahne hodnoty  jses ve fazi 1c.
jses ve fazi 1c.
Faze 1c: Resis ODR (31) pomoci RK4, pricemz postupne pomoci NM aplikovane na (30) dopocitavas 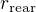 . Pokracujes dokud neni
. Pokracujes dokud neni 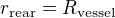 .
.
Pripad 2:
Faze 2a: Opet zacnes resit ODR (23) pomoci RK4, pricemz postupne pomoci NM aplikovane na (22) dopocitavas 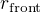 . Jakmile
. Jakmile 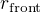 dosahne hodnoty
dosahne hodnoty 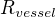 jses ve fazi 2b.
jses ve fazi 2b.
Faze 2b: Resis ODR (34) pomoci RK4, pricemz postupne pomoci (33) dopocitavas konstantu  . Pokracujes dokud neklesne
. Pokracujes dokud neklesne  na nulu.
na nulu.
Faze 2c: Opet resis ODR (31) pomoci RK4, pricemz postupne pomoci NM aplikovane na (30) dopocitavas 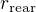 . Pokracujes dokud neni
. Pokracujes dokud neni 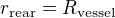 .
.
-----------------
Runge-Kuttovu metodu ctvrteho radu (RK4) a Newtonovu metodu (NM) naleznes napr. v Matlabu, jejich popis je ale vsude mozne na netu a urcite je na par radcich zvladnes naprogramovat sam.
Konkretni postup:
Napr. algebraicko-diferencialni soustavu rovnic (30)+(31) ve fazi 1c resp. 2c muzes resit tak, ze udelas jeden krok RK4 v ODR (31) (tj. spocitas hodnotu tlaku na nove casove vrstve s vyuzitim hodnoty 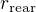 z predchozi casove vrstvy). Nasledne tuto novou hodnotu tlaku pouzijes v rovnici (30) a pomoci NM vypocitas hodnotu
z predchozi casove vrstvy). Nasledne tuto novou hodnotu tlaku pouzijes v rovnici (30) a pomoci NM vypocitas hodnotu 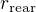 na nove casove vrstve, atd.
na nove casove vrstve, atd.
Offline
#3 23. 09. 2020 15:26
Re: Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
Můžeš pro začátek použít i jednodušší metodu než jen Runge-Kutta. Můžeš třeba použít Eulerovu metodu - sice není tak přesná, ale pro začátek by to mohlo stačit. Vůbec nic na tom není, nejspíš by to šlo udělat i v excelovské tabulce.
Když máš diferenciální rovnici typu 
(jestli tomu rozumím, tak to je přesně to co máš řešit ... složitá jen jen tak funkce F(p), tedy celá ta pravá strana)
no tak z ní uděláš diferenční rovnici - prostým nahrazením nekonečně malými elementy konečně malými, tedy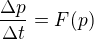
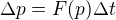

To  musíš vzít nějaké hodně malé (když nevíš jaké, tak ho budeš zmenšovat tak dlouho, až už se výsledek moc nemění), zvolíš nějaké p0 a pak už celý proces jen pořád dokola opakuješ...
musíš vzít nějaké hodně malé (když nevíš jaké, tak ho budeš zmenšovat tak dlouho, až už se výsledek moc nemění), zvolíš nějaké p0 a pak už celý proces jen pořád dokola opakuješ...
Runge-Kuttova metoda je v principu to samé, akorát ten vzoreček jak z  udělat
udělat 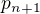 je trochu složitější.
je trochu složitější.
Pro začátek si také můžeš zvolit nějakou jednodušší funkci F(p),
Offline
#4 01. 10. 2020 10:50
Re: Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
Děkuji Vám mnohokrát, pánové, za navedení správným směrem. Zkusím to nějak splácat a snad uvidím, jakou odchylku má tento model pro výbuchy prachů od praktické realizace výbuchů hybridních směsí.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Runge-Kutta čtvrtého řádu a Newton-Raphson pro hledání kořenů
