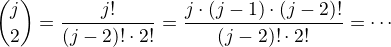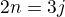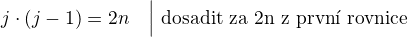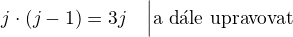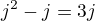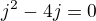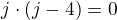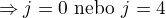Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 02. 2021 00:40
Vénovy diagramy
Nevěděl by někdo?
Na informačním středisku je zaměstnáno několik informátorů - každý ovládá 2 cizí jazyky. Každým z cizích jazyků mluví 3 informátoři. Každou z možných kombinací dvou jazyků mluví jeden informátor. Kolik je na středisku informátorů a kolika cizími jazyky mluví?
Pokud bych počítala, že jazyky jsou tři, vycházelo by mi to 6 zaměstnanců a 3 jazyky. Ale tak jednoduché to nebude ... :D
Offline
#2 24. 02. 2021 07:29
Re: Vénovy diagramy
↑ anterii:
Když označím počet jazyků 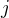 a počet zaměstnanců
a počet zaměstnanců  , musí podle zadání platit
, musí podle zadání platit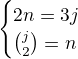
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 24. 02. 2021 15:01 Příspěvek uživatele anterii byl skryt uživatelem anterii.
#4 25. 02. 2021 13:11
Re: Vénovy diagramy
↑ anterii:
Hezký den.
Máte vyřešit soustavu dvou rovnic ↑ zdenek1: o dvou neznámých n, j. Ve druhé rovnici je třeba vyjádřit kombinační číslo [mathjax]{j\choose2}[/mathjax] pomocí faktoriálů Odkaz a po úpravě bude soustava poměrně jednoduchá.
Je s něčím problém?
Pokud se tedy nemýlím.
Offline
#6 26. 04. 2021 16:12
Offline
#8 26. 04. 2021 18:08
Offline
#10 27. 04. 2021 03:05 — Editoval Jj (27. 04. 2021 03:16)
Re: Vénovy diagramy
↑ anterii:
Uvedený zlomek lze krátit (tj. dělit čitatele i jmenovatele) výrazem (j-2)!, ->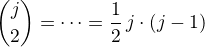
Takže řešit soustavu rovnic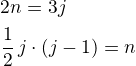
Pokud se tedy nemýlím.
Offline
#14 29. 04. 2021 04:54 — Editoval Jj (29. 04. 2021 05:09)
Re: Vénovy diagramy
↑ anterii:
No, ta je zřejmá z odpovědi kolegy ↑ zdenek1: po vyjádření kombinačního čísla [mathjax]{j \choose 2}[/mathjax] pomocí faktoriálů (↑ Jj:):
Pokud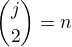
a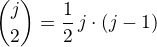
tak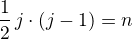
Pokud se tedy nemýlím.
Offline