Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určení složek komplexního čísla, daného složitým výrazem
#3 06. 03. 2021 13:42
Re: Určení složek komplexního čísla, daného složitým výrazem
laszky napsal(a):
↑ 2M70:
Ahoj, v tech vyslednych vztazich pro [mathjax]x[/mathjax] a [mathjax]y[/mathjax] chybi [mathjax]a[/mathjax], coz by asi nemelo, ne?
Máš pravdu, teď na to koukám. Leda že by autor zadání místo  psal omylem
psal omylem  .
.
Offline
#4 06. 03. 2021 14:13 — Editoval Richard Tuček (06. 03. 2021 14:16)
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: Určení složek komplexního čísla, daného složitým výrazem
Pozor: logaritmus v komplexním oboru je víceznačný
ln z =ln(abs(z)*e^(i*arg+2ki pi)=ln(abs(z))+i*arg+2ki pi (k je celé číslo)
exp(a+i b)=(y+i(x+a))/(y+i(x-a))
exp(a+i b)=exp(a)*(cos(b)+i sin(b))
Offline
#5 06. 03. 2021 14:16
Re: Určení složek komplexního čísla, daného složitým výrazem
Richard Tuček napsal(a):
Pozor: logaritmus v komplexním oboru je víceznačný
ln z =ln(abs(z)*e^(i*arg+2ki pi)=ln(abs(z))+i*arg+2ki pi (k je celé číslo)
exp(alfa+i beta)=(y+i(x+a))/(y+i(x-a))
Souhlasím, ale tady se pravděpodobně jedná o hlavní větev logaritmu (Ln z).
Offline
#8 06. 03. 2021 15:08
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: Určení složek komplexního čísla, daného složitým výrazem
To není špatný nápad.
Offline
#10 06. 03. 2021 18:47 — Editoval Richard Tuček (06. 03. 2021 18:50)
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: Určení složek komplexního čísla, daného složitým výrazem
Také by šlo toto:
e^alfa*(cos beta + i sin beta)*(y + i(x-a))=y+i(x+a)
Levou stranu roznásobit a porovnat reálnou a imaginární část.
Dostaneme soustavu 2 rovnic o 2 neznámých a řešit přes determinanty
Je to ale zapeklitý příklad.
Offline
#12 06. 03. 2021 20:48 — Editoval Brano (06. 03. 2021 21:43)
Re: Určení složek komplexního čísla, daného složitým výrazem
EDIT: nevsimol som si ze je tam prehodeny vyznam x a y; definujme teda 
ak  potom
potom  a teda
a teda 
mozme skusit dosadit trebars 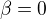 a dostaneme
a dostaneme  , cize
, cize  a
a  - wolfram hovori, ze to sedi, takze to len treba nejak dokopat
- wolfram hovori, ze to sedi, takze to len treba nejak dokopat
Offline
#14 06. 03. 2021 21:45 — Editoval Brano (06. 03. 2021 22:05)
Re: Určení složek komplexního čísla, daného složitým výrazem
↑ laszky:
ospravedlnujem sa za EDIT - ked som si vsimol chybu, tak som si nevsimol, ze si uz napisal odpoved, nebol by som zmenil prispevok.
teraz nam uz iba chyba dokoncit vseobecny pripad
teda tuto ↑ laszky: to mas overene, ale aj tak by bolo pekne mat vyjadtenie priamym postupom a nie spatnym dosadenim riesenia
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určení složek komplexního čísla, daného složitým výrazem
 ,
, 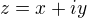
















 ,
,


