Matematické Fórum

Johana16 · 20. 04. 2021 12:26

Dobrý den,
prosím o pomoc s vyřešením této soustavy rovnic v C.

[mathjax]
x^{3}+xy^{2}=10
[/mathjax]

[mathjax]
y^{3}+x^{2}y=5
[/mathjax]

Druhou rovnici jsem vynásobila 2 ->[mathjax]
2y^{3}+2x^{2}y=10
[/mathjax]

A dala tyto rovnice dohromady:

[mathjax]
x^{3}+xy^{2}=2y^{3}+2x^{2}y
[/mathjax]

Upravila na tvar:
[mathjax]
x^{3}-2x^{2}y+xy^{2}-2y^{3}=0
[/mathjax]

[mathjax](x-2y)(x^{2}+y^{2})=0
[/mathjax]

Nyní mám tedy možnost:
a)[mathjax]x-2y=0[/mathjax]
kde jsem si vyjádřila x=2y a to poté dosadila do první původní rovnice -> y=1 a poté dopočetla x=2
První kořen [2,1]

b)[mathjax]x^{2}+y^{2}=0[/mathjax]
Mohla bych si opět vyjádřit [mathjax]x^{2}=-y^{2}[/mathjax]
Zde nastává problém. Nevím, jak vyjádřit x a jak s ním dále počítat.

Platí:[mathjax]x=\pm y\cdot i[/mathjax] ?

Ferdish

Zdravím, áno, na množine komplexných čísiel platí vzorec [mathjax]x^{2}+y^{2}=(x+iy)(x-iy)[/mathjax], skús ho využiť.

Johana16 · 22. 04. 2021 08:08

↑ Ferdish:
Dobrý den, mohla bych Vás poprosit o další nápovědu? Stále nad tím přemýšlím, ale nemohu si vzpomenout, jak by se mělo dál řešit. Děkuji!

surovec

↑ Johana16:
Vem třeba první rovnici a vynásob ji [mathjax]\frac{y}{x}[/mathjax]. Porovnáním s druhou rovnicí získáš [mathjax]x=2y[/mathjax]. Dosadíš do jedné z rovnic a výsledek je [mathjax]y=\sqrt[3]{1}[/mathjax], samozřejmě v komplexním oboru, takže tři řešení. To už dáš, ne?

Ferdish · 22. 04. 2021 09:46

↑ surovec:
A mne sa to hneď nezdalo, že by [mathjax]y^{3}=1[/mathjax] v [mathjax]\mathbb{C}[/mathjax] mala len jedno, rýdzoreálne riešenie :-) je vidieť že keď človek nejaký princíp dlho nepoužíva, tak mnohé veci si musí znova pripomenúť.

Johana16

↑ surovec:

Dobrý den, moc děkuji za radu. Už jsem získala všechny 3 kořeny z [mathjax]y=\sqrt[3]{1}[/mathjax].
Mohu se ale přesto na něco zeptat? Celou dobu jsem pracovala s částí a) [mathjax]x-2y=0[/mathjax]. S částí b)[mathjax]x^{2}+y^{2}=0 [/mathjax] už poté nepracuji? Z jakého důvodu? Případně jaký by byl zde postup?

Děkuji za pomoc

zdenek1 · 22. 04. 2021 13:34

↑ Johana16:
Protože 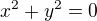$x^2+y^2=0$ není řešení. Když z první rovnice vytkneš $x$ , dostaneš $x(x^2+y^2)=10$ , takže $x^2+y^2$ prostě nemůže být nula.