Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Signatúra, kvadraticka forma (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 05. 2021 21:39
Signatúra, kvadraticka forma
Ahojte, potrebujem pomoc s týmto zadaním.
a)V závislosti od hodnoty parametra  zistíte signatúru matice A
zistíte signatúru matice A



b)Nájdite rozklad kvadratickej formy  na úplne štvorce.
na úplne štvorce.
V časti a) viem len to, že ak 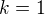 , vtedy matica A je singulárna a má vlastnú hodnotu nula, a ešte to, že matica A nemôže byť kladne alebo zaporne definitná.
, vtedy matica A je singulárna a má vlastnú hodnotu nula, a ešte to, že matica A nemôže byť kladne alebo zaporne definitná.
V časti b) chcem urobiť spektralný rozklad, ale nemôžem nájsť vlastné hodnoty, ak hľadám determinant matice, tak potom mám kubickú rovnicu a neviem ju nejako vyriešiť.
Offline
- (téma jako vyřešené označil(a) Kart)
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Signatúra, kvadraticka forma (TOTO TÉMA JE VYŘEŠENÉ)



