Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 05. 2021 20:49
Vrh koulí s odrazem
Mıcek zanedbatelnych rozmeru o hmotnosti m je vrzen s pocatecnı rychlostı v0 pod uhlem
β z plosiny vysky h tak, ze se na nı odrazı v bode A se soucinitelem restituce ε a dopadne
ve vzdalenosti d od paty plosiny (bod B). Urcete velikost pocatecnı rychlosti
v0 a souradnice odrazoveho bodu A tak, aby mıcek po odrazu dopadl do zadaneho bodu
B. Zanedbejte odpor vzduchu a pri razu neuvazujte trenı ani tıhu mıcku.
Dano:
m = 0, 15 kg
g = 9, 81 m/s2
β = 80◦
ε = 0, 2
l = 3 m
h = 3 m
d = 1, 5 m
rovnice pro souřadnice odrazového bodu A mám vyřešené. Rychlost jsem počítal přes průsečík trajektorie míčku s podlahou, ale nějak mi to nevychází. Díky za rady.
Obrázek k zadání když tak pošlu zvlášt píše mi to, že obrázky nejdou momentálně nahrát.
Offline
#3 01. 06. 2021 10:47
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Vrh koulí s odrazem
Zdravím,
obrázky možno vkladať tiež štandardným postupom - využitím webového úložiska alebo image hostingu a následne umiestnením odkazu, alebo priameho odkazu s využitím tagu IMG (viď lišta pod oknom, kde píšeš text príspevku).
Offline
#6 01. 06. 2021 18:43
Re: Vrh koulí s odrazem
↑ Stepy2:
Otázka je, co potřebuješ. Podle mě jsou všechny nabízené výsledky špatně.
Jediný fyzikální problém, který bys mohl mít, je určení elevačního úhlu v bodě A. Ale podle ZZhyb. se musí zachovávat x-ová složka rychlosti (v tom směru nepůsobí - podle zadání - žádné síly). Takže musí platit , takže
, takže 
Vše ostatní jen počty.
Připojuju Odkaz
 v odkazu je tvoje
v odkazu je tvoje 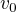
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 02. 06. 2021 01:20
Re: Vrh koulí s odrazem
↑ zdenek1:
Dopracoval jsem se k těmhle rovnicim, ale na konci když spolu porovnám trajektorie tak tam mám pořád vo i v rovnici ... nevim jak dál... mělo by se zjistit nejdřív vo a potom dopočítat zbytek .
https://ibb.co/2jQgsw6
https://ibb.co/T00wckb
https://ibb.co/ZWQbbdK
https://ibb.co/5xLf3jN
https://ibb.co/28ZZv5Y
Offline
#8 02. 06. 2021 01:26
Re: Vrh koulí s odrazem
Ta poslední fotka je špatně konečná rovnice je tahle
https://ibb.co/0yWJCL1
Offline
#9 02. 06. 2021 07:44
Re: Vrh koulí s odrazem
↑ Stepy2:
a) rovnici pro 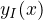 máš dobře, jen bych ji přepsal do tvaru
máš dobře, jen bych ji přepsal do tvaru  - ono se to lépe počítá, když je tam jen jedna goniometrická funkce. ALe to je detail.
- ono se to lépe počítá, když je tam jen jedna goniometrická funkce. ALe to je detail.
b) u bodu dopadu  máš špatně znaménko na pravé straně, a tím pádem i výsledek.
máš špatně znaménko na pravé straně, a tím pádem i výsledek.
c) Musíme si zřejmě ujasnit, jak máte definovaný koeficient restituce. Bez toho se zřejmě nedomluvíme. Normálně je to 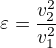 .
.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 02. 06. 2021 14:47
Re: Vrh koulí s odrazem
Na konci by měla vyjít podle výpočtů tahle rovnice (odkaz), ale příklady se musejí dát vyřešit z hlavy na papír takže mi přijde divný, že by na konci vyšla takhle složitá rovnice. Navíc výsledek stejně nevyšel. Něco tam musí být špatně ... někde se tam musí určitě něco pokrátit jen to nevidím.
To
https://www.wolframalpha.com/input/?i=x … 9%29%29%29
Offline
 ?
? . Ne jak je to podle tebe, ale jak to máte ve skriptech, nebo jiných materiálech.
. Ne jak je to podle tebe, ale jak to máte ve skriptech, nebo jiných materiálech.