Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica na tretiu sa rovná 0 (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 08. 2021 21:33 — Editoval sjaustirni (10. 08. 2021 21:44)
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Matica na tretiu sa rovná 0
Zdravím,
pasujem sa s týmto zadaním:
Nech  je
je 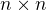 matica v
matica v  a
a  identity matrix typu
identity matrix typu  .
.
Dokáž, že ak 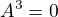 , potom
, potom  a
a  sú inverzné.
sú inverzné.
Kebyže  je pevné dané, dajme tomu 2, tak si zoberiem matrix
je pevné dané, dajme tomu 2, tak si zoberiem matrix ![kopírovat do textarea $A = \left[ {\begin{array}{cc}
a & b \\
c & d \\
\end{array} } \right]$](/mathtex/6d/6df3f6aecd552613735b686efdd0d145.gif)
a zistím, čo vieme povedať o a, b, c a d. Avšak otázka sa týka hocijakého matrixu 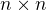 , čo mi napovedá, že mi uniká nejaká vlastnosť square matrixov, inverzie alebo identity matrixov.
, čo mi napovedá, že mi uniká nejaká vlastnosť square matrixov, inverzie alebo identity matrixov.
Mohol by som poprosiť o hint?
BTW tento príklad je v knihe uvedený pred tým, než je ukázaný postup výpočtu inverznej matice, avšak je ukázané na príklade a intuitívne, že ak  , tak
, tak 
Offline
- (téma jako vyřešené označil(a) sjaustirni)
#4 10. 08. 2021 22:56
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Re: Matica na tretiu sa rovná 0
Super, krásne sa to porušilo a zostal mi identity matrix, čo znamená, že dve zátvorky v pôvodnej multiplikácii sú inverzné. Vďaka!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica na tretiu sa rovná 0 (TOTO TÉMA JE VYŘEŠENÉ)
