Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Funkce z Horní Bečvy (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 11. 2009 14:48
Funkce z Horní Bečvy
Najděte spojitou funkci definovanou na intervalu [0,1], která je nulová na Cantorově množině a nenulová mimo ní.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#2 02. 11. 2009 15:09 — Editoval BrozekP (02. 11. 2009 15:18)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce z Horní Bečvy
Sestrojím funkční hodnotu  v bodě
v bodě  mimo Cantorovu množinu:
mimo Cantorovu množinu:
Doplněk Cantorovy množiny  do množiny
do množiny ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) je otevřená množina (Cantorova množina je totiž uzavřená.). Existují tedy takové intervaly
je otevřená množina (Cantorova množina je totiž uzavřená.). Existují tedy takové intervaly ![kopírovat do textarea $(a, b)\subset[0,1]\setminus C$](/mathtex/2c/2c11e3e46b3e0bc9b22c75c8148fa4b9.gif) , že
, že  . Vezmu
. Vezmu 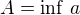 a
a 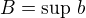 z takových
z takových  , jak jsem popsal. Zřejmě
, jak jsem popsal. Zřejmě 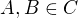 . Je tedy zřejmé, že pro každé
. Je tedy zřejmé, že pro každé 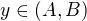 bych našel stejné body
bych našel stejné body  a
a  a proto následující definice bude korektní:
a proto následující definice bude korektní:![kopírovat do textarea $f(x)=\textrm{e}^{-\tan^2\[\frac{\pi}{B-A}\(x-\frac{A+B}{2}\)\]}\qquad\qquad \textrm{pro}\qquad x\in(A,B)$](/mathtex/3b/3ba95a97a275f45a057fc053a5c64394.gif)
A mám ji dokonce hladkou :-)
Offline
#3 02. 11. 2009 15:11
Re: Funkce z Horní Bečvy
Offline
#4 02. 11. 2009 16:16 — Editoval Pavel (02. 11. 2009 16:21)
Re: Funkce z Horní Bečvy
↑ Rumburak:
Pěkné řešení.
↑ BrozekP:
Taky by to šlo, ale ta infima a suprema by musela být zapsána jinak. Já bych vzal 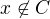 a posloupnost všech otevřených intervalů
a posloupnost všech otevřených intervalů 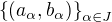 , kde
, kde  je nějaká indexová množina, tak, že
je nějaká indexová množina, tak, že 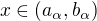 a
a 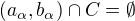 pro
pro 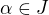 . Pak položme
. Pak položme 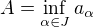 a
a 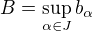 .
.
Pak by stačilo položit .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 02. 11. 2009 16:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce z Horní Bečvy
↑ Pavel:
Tvůj zápis vyjadřuje přesně to, co jsem myslel. Chtěl jsem si ušetřit práci, tu část věty "z takových  , jak jsem popsal" jsem myslel tak, že k zápisům infima a suprema je potřeba dodat, co a a b znamenají, tedy něco jako
, jak jsem popsal" jsem myslel tak, že k zápisům infima a suprema je potřeba dodat, co a a b znamenají, tedy něco jako .
.
Kdybych použil ,
,
nemohl bych pak napsat, že výsledná funkce bude hladká funkce :-) (Ale abych pravdu řekl, nedokazoval jsem si, že ta co jsem napsal má všechny derivace v A, B rovny nule, pouze to tuším.)
(Hladkou tedy myslím ![kopírovat do textarea $C^{\infty}([0,1])$](/mathtex/aa/aa66345455404ece7cd4eace9455acb4.gif) .)
.)
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Funkce z Horní Bečvy (TOTO TÉMA JE VYŘEŠENÉ)
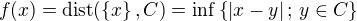
 .
.