Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 11. 2009 17:05 — Editoval Mohammed (24. 11. 2009 17:11)
Kinematika
Zdravim, pomohli by ste mi prosim s tymto prikladem
Objímka se posouvá podél vodorovné tyče s čepem (h=7m), který se pohybuje
v otvoru ramene AB. Obr. K-4. Rameno se kýve s polohovým úhlem φ(t)= 90-30 cos
t. Určete hodnotu ρ(t), složky rychlosti vρ(t)a vφ(t), složky zrychlení aρ(t) a aφ(t),
Ověřte, že výsledný vektor rychlosti a zrychlení bude ležet ve směru vodorovné tyče
např. pro čas t (volte v rozmezí 4÷6) s.
Offline
#2 24. 11. 2009 17:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kinematika
↑ Mohammed:
Zdravím,
jen takový nástin - je potřeba vytvořit funkci polohy čepu na objimce r nejdřív v závislosti na velikosti úhlu  (vhodně zvolena souřadnicová soustava - pravděpodobně s počátkem v bodě A, goniometrická funkce, vhodně zvolený pravoúhlý trojuhelník), úhel se mění v závislosti na čase, tak dojdeš k funkci r(t).
(vhodně zvolena souřadnicová soustava - pravděpodobně s počátkem v bodě A, goniometrická funkce, vhodně zvolený pravoúhlý trojuhelník), úhel se mění v závislosti na čase, tak dojdeš k funkci r(t).
Zkus pouvažovat hraniční polohy ramena s otvorem (např. vertikální atd.).
Až sestavíš rovnici pro r(t), budeš postupovat podobně jako kolega zde: http://forum.matweb.cz/viewtopic.php?id=12075
Offline
#5 24. 11. 2009 19:50 — Editoval zdenek1 (25. 11. 2009 07:57)
Re: Kinematika
↑ Dvorka:
Vyjádříš si  ,
,  (pozor, Mohamed to má špatně)
(pozor, Mohamed to má špatně)
Nyní upravíš  (používat stupně je čuňárna)
(používat stupně je čuňárna)
Určení příslušných rychlostí = derivovat![kopírovat do textarea $v_r(t)=\frac{dr}{dt}=\frac{d}{dt}\left[\frac{h}{\cos(\frac\pi6\cos t)}\right]=$](/mathtex/cd/cd2939369a5affa706ebd532b7853005.gif) spočítáš sám(a)
spočítáš sám(a)![kopírovat do textarea $v_\varphi(t)=r\frac{d\varphi}{dt}=r\frac{d}{dt}[\frac\pi2-\frac\pi6\cos t]=$](/mathtex/95/95ac532e111cb22e127e6d9bb66850ef.gif) spočítáš
spočítáš
Zrychlení = derivovat rychlosti
![kopírovat do textarea $a_\varphi=\frac1r\cdot\frac{d}{dt}[r^2\frac{d\varphi}{dt}]$](/mathtex/b2/b27d53f29b03124c4558032f482d15e7.gif)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 25. 11. 2009 18:34
Re: Kinematika
↑ Mohammed:
Čím? Těma vzorečkam jo, ty jsem opsal z knížky.
Vyjádřením  taky, to je 9. třída
taky, to je 9. třída
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 25. 11. 2009 21:15
Offline
#11 29. 11. 2009 17:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kinematika
↑ Morane:
Zdravím,
derivovali jsem tady: http://forum.matweb.cz/viewtopic.php?id=12237 (není to ovšem upravěno, jen derivace). Překontroluj, prosím, zda se shodujeme. Počítaš v_r jako derivaci složené funkce (mám pocit, že se v tom lišime). Děkuji.
Offline
#12 29. 11. 2009 18:19 — Editoval zdenek1 (30. 11. 2009 16:35)
Re: Kinematika
Jak zjistím .....
Předpokládám, že už máš zderiviváno.

Z obrázku (výslednice je modrá) vidíme, že  což po dosazení dává
což po dosazení dává 
Dále platí  , takže
, takže  a to znamená, že přímky
a to znamená, že přímky  a
a  jsou rovnoběžné.
jsou rovnoběžné.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#15 29. 11. 2009 20:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kinematika
↑ Mohammed:
Nech toho, laskavě - buď spolupracujte a naskenujte vy, co máte - zde ve dvou tématech máte materiálů víc než dost.
Offline
#16 30. 11. 2009 16:04
Re: Kinematika
↑ zdenek1: chci se zeptat, jak by vypadaly derivace pro zrychlení... mám výsledky, ale myslím si, že nejsou správné
Offline
#17 30. 11. 2009 16:08
Re: Kinematika
↑ zdenek1: dosadil jsem do tohoto vzorce  a místo tvého
a místo tvého  mi v čitateli vyšlo sin t .... je tvůj výsledek správný????
mi v čitateli vyšlo sin t .... je tvůj výsledek správný????
Offline
#19 30. 11. 2009 16:42
Re: Kinematika
↑ zdenek1: a nemohl by jsi mi sem dát ještě ty derivace pro zrychlení? Docela by se hodily..
Offline
#22 30. 11. 2009 16:54
Re: Kinematika
↑ zdenek1: a je toto dobře???  , to r se nederivuje? To se bere jako konstanta???
, to r se nederivuje? To se bere jako konstanta???
Offline
#23 30. 11. 2009 16:56 — Editoval zdenek1 (30. 11. 2009 16:56)
Re: Kinematika
↑ Dvorka:
Jinak existuje stránka "wolframalpha.com" a když na ní budeš chvíli hledat, tak je tam derivování (teda ten program derivuje) a i ukazuje jednotlicé kroky ("show steps"). Tak to zkus tam.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline



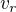 mi vypadlo
mi vypadlo 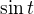 , už jsem to opravil. Zbytek je dobře.
, už jsem to opravil. Zbytek je dobře. a z toho tedy plyne, že
a z toho tedy plyne, že