Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#27 20. 12. 2009 10:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava limity
↑↑ Wentworth:
návrh kolegy ↑↑ jarrro: bych si ani nedovolila komentovat, nepochybuji, že je v pořadku - jen jsem opatrná v použití vzorců, kde se předpokladá použití absolutní hodnoty goniometrických funkci, proto bych rozšířovala tak dlouho, až bych se dopracovala k nečemu takovému:
Z x^2 v čitateli použiji x do pozoruhodné limity 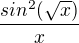 , další x v čitateli zůstává a celou limitu úspěšně obrátí v nulu.
, další x v čitateli zůstává a celou limitu úspěšně obrátí v nulu.
Z náhledu vidím, že milý kolega halogan (pozdrav :-) již doporučuje další pozoruhodnou limitu z toho seznamu, i tak je možné.
----
а зачем Париж?
Offline
#28 20. 12. 2009 18:07 — Editoval Wentworth (20. 12. 2009 18:09)
Re: úprava limity
↑ jelena:
Dekuju moc! Hlavne za ten odkaz, nemel jsem paru o dvou limitach. Chtel bych se optat na tuto pozoruhodnou limitu, kdyz se x blizi k nule zprava (nebo lepe proste k nule), tak co dava za vysledek? 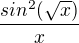
Mohli byste mi nekdo potvrdit muj vysledek, prosim vas u tohoto prikladu..

Offline