Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 12. 2009 17:56
Slovná úloha
Tri bagre A, B, C mali vykopať veľkú jamu. Najprv kopal stroj A toľko hodín, koľko by trvalo spoločne strojom B, C, aby vykopali polovicu tejto jamy. Potom kopal stroj B toľko hodín, koľko by trvalo spoločne strojom A, C, aby vykopali polovicu tejto jamy. Nakoniec kopal stroj C toľko hodín, koľko by trvalo spoločne strojom A, B, aby vykopali polovicu tejto jamy. Takto vykopali celú jamu. Koľkokrát rýchlejšie by ju vykopali, keby pracovali spoločne a nie po jednom?
Pokúšal som sa ju vyriešiť pomocou rovníc, ale k ničomu normálnemu som nedospel.
Slovenčina snáď nevadí.
Offline
#2 24. 12. 2009 23:45 — Editoval jelena (24. 12. 2009 23:48)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovná úloha
↑ Lancer:
Zdravím,
označím výkony jednotlivých bagru jako:
a – práce odvede za hodinu 1. bagr
b – práce odvede za hodinu 2. bagr
c – práce odvede za hodinu 3. bagr.
Dle zadání 1. bagr pracoval nějakou dobu x, za stejnou dobu dokažou druhý a třetí bagr odvést polovinu celé práce, proto: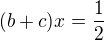
Obdobne plati: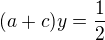
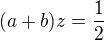
Secteme leve strany rovnic a pravés trany rovnic: 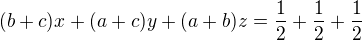 (1)
(1)
Pokud by pracoval každy samostatne po dobu dle zadání (postupně na sebe navazuji), tak celá prace bude hotová: 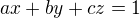
Pokud by pracovali spolu po spolecnou dobu d, platí 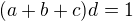
Teď provedu takové úpravy:
prictu k rovnici (1) nalevo a napravo to, co je v rámečku: 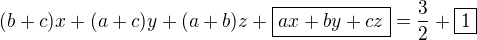 , po uprave
, po uprave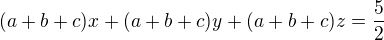
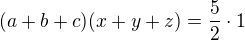 nahrazuji
nahrazuji 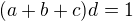
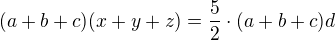 , delim levou a pravou (a+b+c) (predpokladam, ze neni nulovy)
, delim levou a pravou (a+b+c) (predpokladam, ze neni nulovy)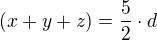 , odsud zjistim pomer doby
, odsud zjistim pomer doby 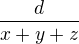
Určitě existuje i nějaké hezčí řešení a také doufám, že jsem neprovedla žádný nepovolený krok. Děkuji za případné napomenutí.
Slovenčina nevadí ani trochu, ale zajimavá doba pro řešení slovních úloh :-)
....
Offline
#3 25. 12. 2009 10:45
- check_drummer

- Příspěvky: 4953
- Reputace: 106
Re: Slovná úloha
↑ Lancer:
Pokud je jáma malá, tak by se jim současně hrabalo jen velmi obtížně. :-)
(Jeden kopáč vykope studnu za hodinu, druhý kopáč za hodinu a půl. Za jak dlouho vykopou studnu společně? :-)
"Máte úhel beta." "No to nemám."
Offline
#4 25. 12. 2009 11:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovná úloha
↑ check_drummer:
Řekla bych, že na velikosti jamy nezáleži - 3 velké bagry budou kopat velkou jamu, 3 malé bagry- malou jamu nebo se mohou kombinovat - otázka byla na "Koľkokrát rýchlejšie by ju vykopali, keby pracovali spoločne a nie po jednom?"
A když už mám přiležitost pohovořit s odbornikem na bagry - v samotném postupu mám nějaký nesmysl? Děkuji a zdravím :-)
Offline
#6 25. 12. 2009 14:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovná úloha
↑ Lancer: já bych si moc nefandila, ale ještě bych počkala na názor kolegy ↑ check_drummer: - umí řešit "Zajímavé příklady a úlohy", je možné, že má hezčí nápad.
Offline
#7 25. 12. 2009 16:16
- check_drummer

- Příspěvky: 4953
- Reputace: 106
Re: Slovná úloha
↑ jelena:
Měl jsem na mysli principielní možnost realizace - zda je vůbec možné, aby 3 bagry při hloubení jámy pracovaly současně? Díky tomu jsem upozornil na úlohu s dvěma kopáči studny, kteří se také dva do studny nevejdou. :-)
"Máte úhel beta." "No to nemám."
Offline
#8 26. 12. 2009 01:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovná úloha
↑ check_drummer: :-) však bagry nejsou ve velké jamě, ale venku okolo - tedy při správném řízení a když jim to vhodně nataktujeme na 3 doby...
Offline