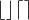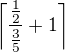Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#901 20. 09. 2012 16:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑↑ user:
Zdravím,
z uceleného pohledu na psaní závorek.
nebo vykopírováno odsud

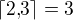
Code:
\lfloor 2{,}3 \rfloor=2
\lceil 2{,}3 \rceil=3Offline
#902 20. 09. 2012 16:38
#903 20. 09. 2012 17:35
#904 21. 09. 2012 22:06
- janca361

- .
- Příspěvky: 3284
Re: LaTeXové pískoviště
Ahoj, potřebuju tohle zadat to WA:![kopírovat do textarea $\frac{(10^{\frac{1}{3}} \cdot 2^{-\frac{3}{2}})^{-3}}{(5^{\frac{1}{2}} \cdot 4^{\frac{1}{8}})^{-2}}:\frac{\sqrt{2 \cdot 2^{\frac{2}{3}}}}{\sqrt[3]{2 \cdot \sqrt[4]{8}}}$](/mathtex/8b/8bdc60cceca21acbffd67b4645e07fe4.gif)
Zadávám to bez $, ale stale mi to nechce vzít a vtrdí mi:
Wolfram|Alpha doesn't understand your query
Showing instead result for query: sqrt
Kde mám chybu? Díky.
Offline
#905 22. 09. 2012 18:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑ janca361:
Zdravím,
co jsem zkoušela WA, se nelibí, když máš 2 odmocniny v jednom zápisu -
Code:
http://www.wolframalpha.com/input/?i=\sqrt[4]{2\cdot+\sqrt[3]{3}}(ani pomocí závorek se mi nepodařilo, ale málo jsem se snažila). Odkazy na WA nevytvořím, protože v zápisu jsou hranaté závorky (někde se to řešilo :-)
tak nevadí:
Code:
\sqrt[4]{2}\cdot \sqrt[3]{3}Tak asi přepsat odmocniny na zlomky:
Code:
(2\cdot \sqrt[3]{3})^{1/4}, pokud potřebuješ. Nebo si vzít jen malý kousek a zkoušet - vadí mu pouze 2. zlomek:![kopírovat do textarea $\frac{\sqrt{2 \cdot 2^{\frac{2}{3}}}}{\sqrt[3]{2 \cdot \sqrt[4]{8}}}$](/mathtex/4d/4d0bafbdd72e60602ead4675d360d3fe.gif)
Proč to potřebuješ přenést do WA právě v takovém zápisu? Děkuji.
Offline
#906 22. 09. 2012 18:50
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: LaTeXové pískoviště
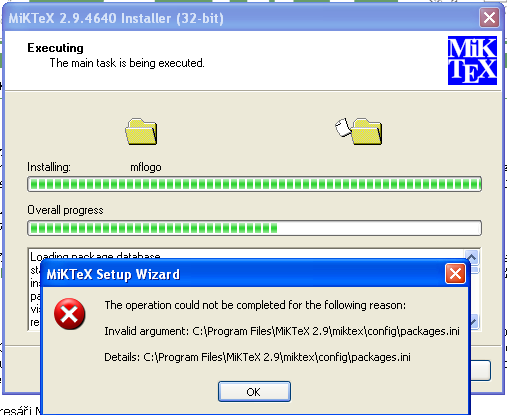
Ahoj, nesetkali jste se někdo při instalaci MiKTeX 2.9 s touhle chybou?
Jelena: doplněno oznámení o vyřešení problému (23.09.2012, 16:39)
Offline
#907 22. 09. 2012 19:44
#908 22. 09. 2012 19:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑ janca361:
a tak - tak se zlomkem se podaří určitě, jen dostatek závorek. Potom to můžeš psát do sekce CAS, kdyby nešlo (doufám, že ne - je tam takový hezký klid :-)
Offline
#909 22. 09. 2012 20:01
#910 23. 09. 2012 12:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑ janca361:
já jsem to brala, že souvisí se zápisem LaTeX, tak snad nevadí. Ale dotaz kolegy ↑ FliegenderZirkus: se asi zatoulá - to bych řekla, že patří jinam, do samostatného tématu.
Offline
#911 23. 09. 2012 12:49
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: LaTeXové pískoviště
↑ jelena:
Teď už vlastně doufám, že se zatoulá, protože dotaz už je vyřešený a nemám kde to odškrtnout. Samostatné téma by bývalo bylo na místě, příště to tak udělám. Pěknou neděli. :)
Offline
#912 23. 09. 2012 16:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑ FliegenderZirkus:
děkuji za přání a za sdělení - to je dobře, v příspěvku jsem provedla záznam o vyřešení problému :-)
Offline
#913 27. 09. 2012 21:55
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: LaTeXové pískoviště
Princip exkluze a inkluze:
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#914 27. 09. 2012 22:08
#915 13. 10. 2012 17:37
#917 14. 10. 2012 12:15
#918 14. 10. 2012 12:20
#920 14. 10. 2012 12:51
Re: LaTeXové pískoviště
↑ Andrejka3: díky, právě také zastávám názor, že to nevypadá nejlépe, prostě to asi převést na desetinné a k tomu hodit "závorky", to vypadá nejlépe (btw, jak se to jmenuje? znak horní celé části?)
wiki říká:
Symboly funkcí mají podobu hranatých závorek, kterým schází dolní či horní vodorovné čárky.
Offline
#921 14. 10. 2012 12:55
#922 17. 10. 2012 16:02
#923 17. 10. 2012 23:58
#924 18. 10. 2012 00:25
Re: LaTeXové pískoviště
Offline
#925 23. 10. 2012 11:23 — Editoval JohnPeca18 (23. 10. 2012 15:40)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: LaTeXové pískoviště






Offline