Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 01. 2010 21:25
Determinant s paramtrem
Zdravím. Rád bych poprosil o pomoc s příkladem, kde se jedná o výpočet linerární nezávislosti vektorů, z nichž některé jsou zadané s parametrem. Vím, že pokud |A|=0 potom mají být vektory lineárně nezávislé, ovšem při výpočtu mi vychází kvadratický člen u výsledku determinantu.
Zadání:
u1 = (t,0,t,0)
u2 = (1,-1,0,0)
u3 = (1,1,1,1)
u4 = (t,2,3,4)
Nejsem si zcela jist, co má být jako výsledek. Počítám, že pravděpodobně hodnota determinantu, ale vždy se dostanu k nějakým dvěma řešením hodnoty parametru t, což asi není to, co bych potřeboval.
Offline
#2 11. 01. 2010 21:30
Re: Determinant s paramtrem
jestlize ti vychazi kvadraticky clen melo by to byt v poradku.potom linearni zavislost bude pro t elementem 2 cisel.To zname kdyz dosadis za t jedno cislo ktere ti vyslo p=ri reseni kvadr rovnice budou vektory zavisle a to same plati i pro druhe cislo (druhe reseni kvadr. rovnice.)
Offline
#3 20. 01. 2010 21:51 — Editoval vaanha (20. 01. 2010 21:51)
Re: Determinant s paramtrem
A jak je to v tomto případě?
Mám zadány vektory 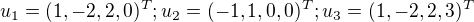 a
a 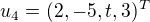
Zadání - urči, pro jaké hodnoty  je vektor
je vektor 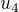 lineární kombinací vektorů
lineární kombinací vektorů 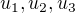 .
.
Při svém postupu vycházím z definice lineární závislosti: 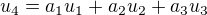 . Poté mi vychází
. Poté mi vychází 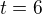 . Je můj postup správný? Nejsem si zcela jistý, zda-li jsem pochopil vysvětlení z předchozího příspěvku.
. Je můj postup správný? Nejsem si zcela jistý, zda-li jsem pochopil vysvětlení z předchozího příspěvku.
Offline