Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 02. 2010 09:38 — Editoval RobbieMan (05. 02. 2010 09:40)
priklady z analyzy
dobre rano,
pri me dlouhe ceste za slozenim zkousky z matanalyzy jsem narazil na par prikladu, ktere i po dlouhe namaze nemohu vyresit, za jakoukoli radu budu velice vdecny konverguje to k nule ale jak to dokazat opravdu netusim
konverguje to k nule ale jak to dokazat opravdu netusim upravit se to da jednoduse na
upravit se to da jednoduse na  ale tam pak obecne nevim co s tim sinem, jak dokazat ze alternuje, podobna rada se sinem se tu objevila ale pouzivalo se tam to "ocko"
ale tam pak obecne nevim co s tim sinem, jak dokazat ze alternuje, podobna rada se sinem se tu objevila ale pouzivalo se tam to "ocko"
dekuji.
Offline
#2 05. 02. 2010 10:13 — Editoval Rumburak (05. 02. 2010 10:24)
Re: priklady z analyzy
Pouze napovím:
B1 . Ukaž, že posloupnost je nazáporná a klesajíci - má tedy nezápornou limitu, kterou označme L.
Ze spojitosti fce sin odvoď, čemu se rovná sin L a pak snadno příjdeš na to, čemu se rovná L.
C1 . Předpokládám, že v definici té posloupnosti je zlomek. S využitím 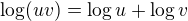 ,
, 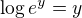 ho upravíme:
ho upravíme: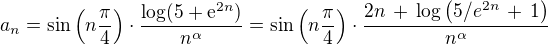 a nový zlomek vydělíme - tím vznikne součet zlomků.
a nový zlomek vydělíme - tím vznikne součet zlomků.
Výraz 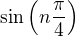 nabývá střídavě pouze několika málo hodnot - kterých ?
nabývá střídavě pouze několika málo hodnot - kterých ?
Ta zbývající úloha je pouze snad pracná, ale se znalostmi definic a základních vět není obtížná.
Offline
#4 05. 02. 2010 14:13 — Editoval Rumburak (05. 02. 2010 14:18)
Re: priklady z analyzy
Myslím, že hledat nějký jednotný inteligentní alg. vzorc pro 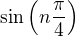 není efektivní, stačilo by uvědomit si, že
není efektivní, stačilo by uvědomit si, že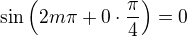 ,
,  ,
,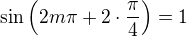 ,
,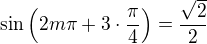 ,
,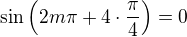 ,
,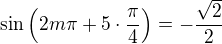 ,
,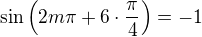 ,
,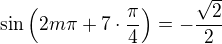
atd. periodicky.
Důlečité jsou dvě vlastnosti této posloupnosti :
1) je omezená,
2) nemá limitu (má celkem 5 hromadných hodnot) .
Offline
#5 06. 02. 2010 18:48
Re: priklady z analyzy
C4 opravdu neni tak tezka, f(x) je vlastne konvexni (monotonni) na celem svem def. oboru tim padem staci zajistit aby limita v nekonecnu byla nekonecno a limita v minus nekonecnu minus nekonecno, a bylo to definovano pro vsechna x z R.
ale stale porad nevim co s tim prvnim prikladem, nejsem si vubec jisty jak mam tu monotonni a nezapornost dokazat,
budu rad za jakoukoli radu, diky
Offline
#6 06. 02. 2010 19:17
Re: priklady z analyzy
Jelikož  , je
, je  . Protože pro
. Protože pro 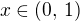 je
je 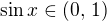 , platí
, platí 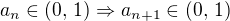 , takže díky indukci
, takže díky indukci  . Monotónnost se dokáže snadno díky nerovnosti
. Monotónnost se dokáže snadno díky nerovnosti  na příslušném intervalu.
na příslušném intervalu.
Offline