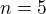Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 02. 2010 16:30
geometrická posloupnost
Prosím o pomoc s tímto problémem: V geometrické posloupnosti s kvocientem q=2 vypočtěte, kolik členů dává součet 186, jestliže poslední sčítanec je 
Zkusila jsem podle vzorce  , ale výsledek není dobrý. Děkuji vám....
, ale výsledek není dobrý. Děkuji vám....
Offline
- (téma jako vyřešené označil(a) leník 5)
#2 11. 02. 2010 16:53
Offline
#3 12. 02. 2010 08:30
Re: geometrická posloupnost
↑ zdenek1: Prosím, můžu požádat o podrobnější zápis? Nezvládám, jak dostanu na levé straně zlomek  a potom, jak vznikne ten další řádek. Děkuji moc.
a potom, jak vznikne ten další řádek. Děkuji moc.
Offline
#4 12. 02. 2010 08:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: geometrická posloupnost
↑ leník 5:
Zdravím, bylo řešeno- je to dostatečně podrobně? (snad tam nemám nějaký překlep)
Offline

 a
a