Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » kvadraticka rovnica s komplexnymi cislami (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 02. 2010 11:08
- princess21
- Příspěvky: 34
- Reputace: 0
kvadraticka rovnica s komplexnymi cislami
dobry den, riesim skusobne testy na VSE a narazila som na problem komplexnych cisiel, ktore sme na strednej skole neprberali,a ako samouk rozumiem iba uplne najzakladnejsim prikladom. potrebovala by som pomoct s nasledujucim prikladom:
Víme-li, že jedním kořenem kvadratické rovnice s reálnymi koeficienty je komplexní číslo x=3+2i, pak tuto rovnici lze napsat ve tvaru....
aj ked je to mozno lahky priklad, ja tomu vazne nerozumiem, ako na to ist. dakujem pekne :)
Offline
- (téma jako vyřešené označil(a) jelena)
#2 21. 02. 2010 11:15
Re: kvadraticka rovnica s komplexnymi cislami
↑ princess21:
Když mákvadratické rovnice s reálnymi koeficienty řešení tvaru 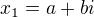 , tak druhé řešení je
, tak druhé řešení je 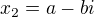 (říká se tomu komplexně sdružená čísla).
(říká se tomu komplexně sdružená čísla).
Rovnice je pak 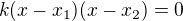 kde
kde 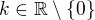
Konkrétně (pro jednoduchost 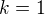 )
)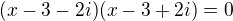
![kopírovat do textarea $[(x-3)-2i][(x-3)+2i]=0$](/mathtex/dc/dc955598286668e8926de2d1a63eda3b.gif) (to je vzorec
(to je vzorec  )
)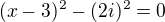
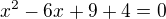
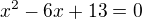
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 21. 02. 2010 11:18
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: kvadraticka rovnica s komplexnymi cislami
U polynomů s reálnými koeficienty platí, že pokud 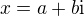 je kořenem polynomu, pak i
je kořenem polynomu, pak i 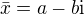 je kořenem polynomu. Důkaz tohoto tvrzení je snadný:
je kořenem polynomu. Důkaz tohoto tvrzení je snadný:
Ať  je kořenem polynomu
je kořenem polynomu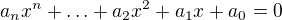 .
.
Rovnost komplexně sdružíme: ,
, jsou reálná čísla, platí tedy
jsou reálná čísla, platí tedy 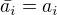 .
.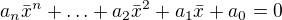
To ale znamená, že 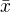 je kořenem polynomu.
je kořenem polynomu.
Offline
#4 21. 02. 2010 11:43
- princess21
- Příspěvky: 34
- Reputace: 0
Re: kvadraticka rovnica s komplexnymi cislami
dakujem krasne za rychlu odpoved, uz mi to je jasnejsie :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » kvadraticka rovnica s komplexnymi cislami (TOTO TÉMA JE VYŘEŠENÉ)