Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2008 17:20
Binomický rozvoj pro x>0
Ahoj,
tak jsem narazil na příklad:
Binomický rozvoj ( 1/x - sqrt(x) )^7 pro x>0 obsahuje člen: ?
Výsledek je 35/x
Je to zadáno jaksi s mocinko více neznámýma než jsem zvyklý, takže to nějak nechápu. Jinak klasický bin. rozvoj třeba pro x^6 chápu.
Díky
Offline
#4 03. 02. 2008 18:32 — Editoval jelena (03. 02. 2008 18:35)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Binomický rozvoj pro x>0
a pak nasleduji moznost vyberu, nebo ne?
http://web.quick.cz/koci.senior/Binom%20veta.htm ten rozklad se provede podobne, ale ktery ze clenu je zrovna zajimavy?
Offline
#6 03. 02. 2008 18:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Binomický rozvoj pro x>0
↑ lopson:
tak to je presne podle navodu, na ktery odkazuji, hledas clen, u ktereho celkova mocnina x bude (-1).
Pokud nepujde, tak se ozvi :-) Hodne zdaru :-)
Offline
#8 04. 02. 2008 18:45
Re: Binomický rozvoj pro x>0
Ahoj,
tak jsem se kukal na ten příklad aaa vyšel mi v pohodě. Pak jsem ještě narazil na podobný příklad pro (x ≠ 0) aaa taky mi vyšel. Avšak chtěl bych se zeptat, zda-li se dají takovéto typy příkladů řešit bez zadaných možností? A to možná co nejrychleji.
Offline
#9 04. 02. 2008 19:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Binomický rozvoj pro x>0
↑ lopson:
:-) resit priklad - to prece znamena, ze odpovidam na nejakou otazku. Pokud nemam otazku, tak nic neresim (alespon ja :-)
Binomicky rozvoj jako takovy podle vzorce muzes udelat pro kazdy rozumne zadany vyraz. Ovsem podle toho jak zni uloha, tak se obvykle hleda nejaky konkretni clen - treba urcit, ktery clen rozvoje je absolutni (tj. neni u neho zadna promenna, mocnina promenne je 0) nebo urcit, ktery clen rozvoje obsahuje nejakou konkretni mocninu nebo konkretni koeficient a podobne).
To, ze tam mas zadane moznosti, to je jen zpusob jak formulovat otazku - tusim se tomu rika odborne "otazka uzavrena alternativni" - zkratka neni kam uhnout a musis vybirat z nabizenych moznosti.
Zkus se podivat do sbirek, jako jeste jsou ulohy z tohoto tematu.
Je to srozumitelne? (otazka otevrena :-)
Offline
#12 28. 02. 2009 18:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Binomický rozvoj pro x>0
↑ aMonia:
Zdravím :-)
toto je zadání z testů na VŠE: http://www.vse.cz/download/cz/zamestnan … zadani.pdf
Každá otázka je postavena tak, že jedina správná odpověď je schovana v nabídce odpovědí uvedených po otázce.
Zadání, které zde rozebírame, - pokud by nemělo nabídku odpovědí, tak by se řešilo tak, že zapiší celý binomický rozvoj výrazu dle postupu binomické věty: http://cs.wikipedia.org/wiki/Binomick%C3%A1_v%C4%9Bta
My ovšem máme nabídku odpovědí - hledáme tekový člen binomického rozvoje , který obsahuje x^(-1)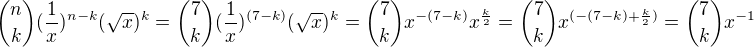
koeficient (7 nad k) ponecháme bez povšímnutí a budeme řešít pouze čast, která obsahuje x (mocniny nad x):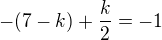
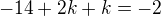
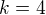
Teď se vrátime k koeficientu: 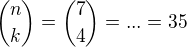
Ještě se podívej na odkaz, který jsem uvedla o pár příspěvků výš.
OK?
------------
Kolega lopson se na VŠE úspěšně dostal a posílám mu hezký pozdrav :-)
Offline