Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » "Jednoduchá" úložka z Jarníka (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 03. 2010 20:59
"Jednoduchá" úložka z Jarníka
Zdravím kolegy, procházím si zadání starších ročníků Jarníka a sleduji, jak mé šance jdou limitně k nule. U jedné úlohy jsem se zasekl dokonce i na jejím řešení - je to trojka tady. Prvotní problém mám s větou
Suppose that for any x > N we have that f(x) and f(N) are of different signs.
Opravdu tam patří to slovo any? Já ho tam totiž chápu ve smyslu libovolné, tedy že to platí pro všechna x > N. To mi ale přijde jako nesmysl vzhledem k tomu, co se snažíme dokázat. Více by se mi tam líbilo slovíčko some.
Potom ještě problém s tou snadnou indukcí. Druhý indukční krok je OK, ale jak přijít na ten první, tj. že  ? Dělal bych to asi takto:
? Dělal bych to asi takto: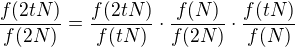
Protože tN > N, je  dále pak
dále pak  , ale o
, ale o 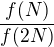 nevíme zhola nic - možná kdyby se na začátku vzalo N tak, že by
nevíme zhola nic - možná kdyby se na začátku vzalo N tak, že by  platilo pro
platilo pro 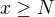 …
…
Prosím pomozte!
Offline
- (téma jako vyřešené označil(a) Olin)
#2 24. 03. 2010 01:29
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: "Jednoduchá" úložka z Jarníka
↑ Olin: Taky bych tam viděl spíš 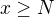 . Co se týče angličtiny, se slovem some mi to zní taky líp (že zde any bylo míněno jako "nějaké" a ne jako "libovolné" je zřejmé).
. Co se týče angličtiny, se slovem some mi to zní taky líp (že zde any bylo míněno jako "nějaké" a ne jako "libovolné" je zřejmé).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » "Jednoduchá" úložka z Jarníka (TOTO TÉMA JE VYŘEŠENÉ)