Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#8 14. 05. 2010 15:36
Re: Funkce
↑ Rumburak:
Co např. takto?
Pak definujme 
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 14. 05. 2010 16:03 — Editoval Rumburak (14. 05. 2010 16:16)
Re: Funkce
↑ Pavel:
Řetězové zlomky jsem nikdy nestudoval, Tebou podaná definice mi připadá věrohodná :-).
Šlo mi o to, že ve středoškolské matematice, do níž tato úloha zde byla zařazena, se ŘT neprobírají - leda snad "nadplán" jako zajímavost -
a jak oba víme, pracovat s infinitezimálními pojmy intuitivně bývá často zrádné. Proto jsem otázku definice nadhodil - a poctivě přiznám,
že sám jsem si chtěl rozšířit obzor, za což díky. :-).
Offline
#12 15. 05. 2010 16:24
Re: Funkce
↑ pietro:
Můžeme toto probrat podrobněji, jen mám obavy, že toto vysoce přesahuje rámec střední školy. Pokud bychom měli být důkladní, tak je třeba nejdříve dokázat, že posloupnost funkcí tak, jak jsem ji definoval, je opravdu konvergentní a specifikovat, pro která x tomu tak je. Bez těchto úvah se bezhlavé použití limitního přechodu tak, jak jsem ho navrhl, může minout účinkem. Jako příklad uvádím
kde limitním přechodem bychom došli k chybnému závěru, že  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#14 15. 05. 2010 17:48
Re: Funkce
↑ Rumburak:
Tento dataz je velmi správný a je jen škoda, že nebyl položen někým jiným již dříve. Výrazům se musí nejprve přisoudit v definicích jejich jedinečný smysl.
Teorie řetězových zlomků dává mimořádně plodné aplikace v oblasti teorie čísel (konstrukce transcendentních čísel, studium diofantických aproximací, řešení Pellovy rovnice a mnoho dalších). Ke studiu řetězových zlomků mohu doporučit Chinčinovu knížku Řetězové zlomky - vyšla i v češtině. Pokud ji neseženete v knihovnách, můžete si ji stáhnout zde (PDF). Další mimořádně zajímavé čtení potom neleznete v Loyově knížce (PDF, free).
Offline
#16 17. 05. 2010 13:05
Re: Funkce
Snad nebudu moc OT, ale chtěl bych vaši diskusi o řetězových zlomcích a (ne)definovaných výrazech obohatit o následující kus:
Zkuste spočítat hodnotu :-)
Offline
#17 17. 05. 2010 13:56
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Funkce
↑ Olin:
Já jsem nepolíbený řetezovými zlomky, ale kdyz zkusím uvažovat logicky, jde o zlomek 1+nekonečně malé číslo / 1-nekonečně malé číslo, v R je nekonečně malé číslo reprezentováno nulou, takže  . Je to jenom logická úvaha, asi nevystihla pravý smysl příkladu, ale logicky vzato by to mělo platit :)
. Je to jenom logická úvaha, asi nevystihla pravý smysl příkladu, ale logicky vzato by to mělo platit :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#18 17. 05. 2010 14:36 — Editoval Rumburak (17. 05. 2010 14:45)
Re: Funkce
Offline
#19 17. 05. 2010 15:52 — Editoval Pavel (17. 05. 2010 15:54)
Re: Funkce
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#21 17. 05. 2010 16:51
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce
↑ Pavel:
Označím
Pro 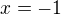 už
už  nemá smysl. Pro ostatní
nemá smysl. Pro ostatní  platí
platí
Aby tedy limita existovala, muselo by platit
To platí pouze pro  . Záleží tedy na tom, s čím začneme.
. Záleží tedy na tom, s čím začneme.
Offline
#22 17. 05. 2010 17:06 — Editoval Pavel (17. 05. 2010 17:06)
Re: Funkce
Přesně tak. Velmi záleží na tom, jaká je počáteční hodnota  . Pro ostatní hodnoty limita neexistuje. Výraz
. Pro ostatní hodnoty limita neexistuje. Výraz  tak, jak je napsán, není korektně definován - není dáno pravidlo, jak jej počítat.
tak, jak je napsán, není korektně definován - není dáno pravidlo, jak jej počítat.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
 .
. ?
?


 ?
?
 by splňovala rovnici
by splňovala rovnici  , odtud
, odtud  , tato rovnice ovšem nemá reálné kořeny.
, tato rovnice ovšem nemá reálné kořeny. 

 nejsou ostatní v reálných číslech definovány (dělení nulou). Tudíž o limitě nemůže být ani řeč.
nejsou ostatní v reálných číslech definovány (dělení nulou). Tudíž o limitě nemůže být ani řeč.


