Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2010 19:48
Suma
Dokážte konvergenciu a nájdite súčet radu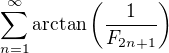
kde  označuje k-te Fibonacciho číslo.
označuje k-te Fibonacciho číslo.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
- (téma jako vyřešené označil(a) lukaszh)
#3 03. 04. 2010 18:24 — Editoval Marian (03. 04. 2010 18:25)
Re: Suma
↑ lukaszh:
Budu postupovat poměrně rychle ...
Dle mého názoru ovšem o algebru nejde (pokud někdo nenajde řešení algebraické).
Offline

 .
.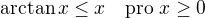
 .
.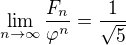 ,
, je zlatý řez (který je větší než 1), je řada konvergentní podle limitního srovnání s
je zlatý řez (který je větší než 1), je řada konvergentní podle limitního srovnání s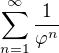 .
.


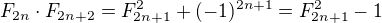 . Odtud a pomocí Cassiniho vzorce s tzv. running sum je možné psát
. Odtud a pomocí Cassiniho vzorce s tzv. running sum je možné psát


 , která je také součtem hledané řady.
, která je také součtem hledané řady.