Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Slovní úlohy řešené pomocí derivací (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 04. 2010 15:05
- maggievici
- Zelenáč
- Příspěvky: 3
- Reputace: 1
Slovní úlohy řešené pomocí derivací
Dostali jsme za domácí úkol vyřešit tuto slovní úlohu (Petáková 161/67) : Do koule o poloměru 3 cm vepište válec o maximálním objemu. Určete jeho rozměry.
Určila jsem si vzorec pro objem a obsah válce, nakreslila nákres, kde je zřejmé, že od středu koule do bodu, kde se jí válec dotýká je 3cm a z toho určila, že 3^2 = r^2 + v^2/4, kde r = poloměr podstavy válce. Z tohoto vzorce jsem vyjádřila v, dosadila do vzorce pro objem, derivovala a vyšlo r = 0 v r = 2. Určila jsem definiční obor D=r náleží (0;6), udělala pomocí tabulky globální maxima a minima ze kterých mi vyšlo maximum v bodě 2, čili r=2, což bohužel není správný výsledek. Nedokážu určit, ve kterém kroku jsme udělala chybu, nebo zda jsem postupovala úplně špatně, proto jsem vám to popsala podrobně. Budu moc ráda za všechny rady.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 18. 04. 2010 16:28 — Editoval Chrpa (18. 04. 2010 16:35)
Re: Slovní úlohy řešené pomocí derivací
↑ maggievici:
Označme: r - poloměr válce
v - výška válce
V objem válce (má být maximální)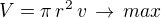
Z Pythagorovy věty platí: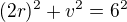 ( průměr válce na druhou + výška válce na druhou = průměr koule na druhou)
( průměr válce na druhou + výška válce na druhou = průměr koule na druhou)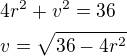 - dosadíme do rovnice pro objem válce:
- dosadíme do rovnice pro objem válce: - toto stačí derivovat a derivaci položit rovnu nule.
- toto stačí derivovat a derivaci položit rovnu nule.
Pokud jsem dobře počítal:
Offline
#3 18. 04. 2010 16:38 — Editoval maggievici (18. 04. 2010 16:54)
- maggievici
- Zelenáč
- Příspěvky: 3
- Reputace: 1
Re: Slovní úlohy řešené pomocí derivací
derivovala jsem, dala do rovnosti s nulou a vyšlo r=0 :(
počítal jsi dobře, ale já pořád ne.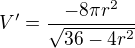
Offline
#4 18. 04. 2010 16:56 — Editoval Chrpa (18. 04. 2010 17:01)
#5 18. 04. 2010 17:53
- maggievici
- Zelenáč
- Příspěvky: 3
- Reputace: 1
Re: Slovní úlohy řešené pomocí derivací
děkuju, už to vychází
Offline
#6 29. 04. 2012 16:33
Re: Slovní úlohy řešené pomocí derivací
↑ maggievici:
Prosím vás, jak vypočítám tu výšku? Děkuji
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Slovní úlohy řešené pomocí derivací (TOTO TÉMA JE VYŘEŠENÉ)


 podstavy válce do
podstavy válce do