Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 27. 02. 2008 16:20 — Editoval robert.marik (27. 02. 2008 16:20)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: neurčitý integrál
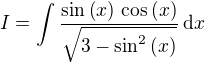
\begin{array}{c}3-\sin ^{2}{\left(x\right)}=t^{2}\\-2\, \cos ^{}{\left(x\right)}\, \sin ^{}{\left(x\right)}\, \mathrm{d}x=2\, t\, \mathrm{d}t\end{array} .... viz substituce
.... viz substituce
Offline
#5 03. 03. 2008 09:47
Re: neurčitý integrál
↑ gyerpal:
řek' bych, že podle další substituce 3-t^2=u, -2tdt=du
100*0>0 aneb stokrát nic umořilo osla
Offline
 dostanes
dostanes