Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 12. 05. 2010 22:23
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Soustavy rovnic
Já už nevím, jak ti to vysvětlit lépe, nechal jsem na tom dost casu, a to nejen já. Víš co? uděláme kompromis: Ty lehčí snad zvládáš, tak si vezmi nějaký z těch těžších, a : bud, umíš-li: Dej sem tvůj postup, jak jsi to počítal - na oplátku ti najdeme chybu (-y) a ukážeme ti, nac o si dát pozor do budoucna. Nebo: napiš to na papír a řeš, pak to oskenuj (nebo vyfot fotakem) a dej to sem jako obrázek (neznáš-li TeX). Nejsme automaty, do kterých hodíš příklady, zatočíš klikou a vypadne řešení, které ti k ničemu stejně nebude :) Takze: ano, sednu si s tebou, dáme to nějak dohromady tak, abys to pokud možno pochopil, ale počítat ti to nebudeme (jestli nekdo z kolegů, ale pochybuju o tom)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#27 12. 05. 2010 22:29 — Editoval Chrpa (12. 05. 2010 22:32)
Re: Soustavy rovnic
↑↑ Veter@n:
Ukážu Ti 2 způsoby na prvním příkladu:
a) metoda dosazovací
b) metoda sčítací(odčítací)
ad a)
1) 
2) 
Při této metodě si vyjádřím jednu proměnnou z jedné té rovnice a toto dosadím do druhé rovnice a vypočítám jednu neznámou.
V tomto případě se jeví jako nejjednodušší vyjádřit proměnnou y z druhé rovnice tedy: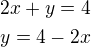 - to dosadím do první rovnice a vypočítám proměnnou x tj:
- to dosadím do první rovnice a vypočítám proměnnou x tj: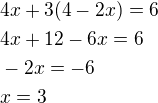
Vypočítanou proměnnou dosadím do tohoto 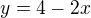 a dopočítám y tj:
a dopočítám y tj: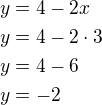
Řešení je 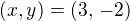
ad b)
Rovnice vynásobím nějakým číslem tak,abych se při sečtení(odečtení) těch 2 rovnic mezi sebou zbavil jedné proměnné a mohl tak dopočíta druhou proměnnou.
Tady vynásobím rovnici 2) číslem minus 3 a sečtu s rovnicí 1) tedy: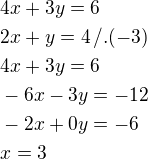
Za x = 3 dosadím do jakékoliv předmětné rovnice a dpočítám y (např. do 1))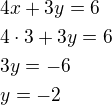
Řešení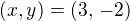
A takto můžeš pokračovat v dalších příkladech.
Offline
#29 13. 05. 2010 00:12
Re: Soustavy rovnic
↑ gadgetka:
dovolím si nesouhlasit že řešení je nekonečno řešením musí bejt uspořádaná dvojice
Offline
#31 13. 05. 2010 00:25
Re: Soustavy rovnic
↑ Mr.Pinker:
oki, souhlasím ... a nechám to na tazateli ... takže je nekonečně mnoho uspořádaných dvojic, to už je lepší závěr?
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#33 13. 05. 2010 01:09
Re: Soustavy rovnic
Pravidlo 4 napsal(a):
Nejsme automat na řešení příkladů.
↑ gadgetka: je třeba říct něco ve stylu "řešením jsou dvojice 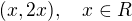 "
"
Offline
#34 13. 05. 2010 01:38
Re: Soustavy rovnic
Děkuji, Stýve ... omlouvám se za porušení pravidel, jsem tu teď častěji vzhledem k tomu, že mám syna v nemocnici po úrazu ... tak abych zatěžovala mozek něčím jiným než přemýšlením, jak to všechno dopadne...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#35 10. 03. 2013 11:11
Re: Soustavy rovnic
Nevím,jak vyřešit rovnici:xΛ4-8xΛ3+x-8=0, neumím vlastně z prvních dvou členů vytknout společný násobek. Díky za pomoc (ve škole jsme to snad probírali, ale já jsem v poslední době dost chyběl).
Offline