Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2010 22:29
Deltoid
Daný je deltoid ABCD s uhlami pri vrcholoch B, C, D po rade 90°, 135°, 90° a dĺžkou uhlopriečky |BD| = sqrt(2) cm. Vypočítajte presne dĺžku uhlopriečky AC.
Úloha je celkom jednuduchá. Avšak táto úloha je určená pre riešenie BEZ kalkulačky. Ďakujem za pomoc
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) byk7)
#2 30. 05. 2010 10:29
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Deltoid
Dobrá, nejdříve brainstorming, potom z toho zkusím udělat nejaký vzorec na výpočet (prostě to zobecním):
Tedy deltoid má vždy dvě přiléhající strany stejně dlouhé - delší úhlopříčka bude půlit úhly při vrcholech A a C. Je to čtyřúhelník, pro každý 4úhl platí že součet vnitřních úhlů je 360°. Delší úhlopříčka vždy půlí tu kratší (já vím, zavádějící definice, myslím v klasickém "konvenčním" deltoidu ve tvaru papírového draka)
Takže, máme celkem 2 páry shodných pravoúhlých trojúhelníků, co potřebujeme je spočítat jednu z odvěsen. To vede na goniometrické funkce, úhly u vrcholů A a C vypadají celkem rozumně, 135 (90+45, tabulková hodnota) a 45 (taky).
Když nesmí být kalkulačka, můžou být tabulky??? Jednodušší cestou potřebuju tangenty polovin úhlů 135 a 45
Mám-li tangenty polovin úhlů, snadno dopočtu přilehlé odvěsny a ty sečtu, mám délku
Další možnost. Hledaná příčka je přeponou pravoúhlému trojúhelníku s pravým úhlem u vrcholu B (D). Znám však jenom výšku na přeponu a všechny tři úhly, které jsou opět půlkami těch hezkých tabulkových.... Ty tabulky by mi hodně pomohly ;)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#3 30. 05. 2010 10:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ frank_horrigan:
Žádné tabulky nejsou potřeba :-).


Teď už stačí dosadit 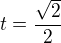 a
a 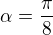 . Sinus úhlu
. Sinus úhlu 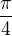 si snad každý pamatuje, případně dokáže odvodit.
si snad každý pamatuje, případně dokáže odvodit.
Offline
#4 30. 05. 2010 10:59
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Deltoid
↑ BrozekP:
Teda, klobouk dolu. Nejsem si úplně jistý, zda žáci ZŠ znají vlastnosti funkce tangents ve vztahu k poměru sinu versus cosinu (sám si to musím malovat, a to předpokládá že "vím co hledám"), ale řešení je to elegantní a moc pěkně udělané :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 30. 05. 2010 11:07
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ frank_horrigan:
Díky. Přehlédl jsem, že to je v sekci ZŠ, možná by se to dalo řešit jinak, teď mě ale nic nenapadá.
Offline
#6 30. 05. 2010 11:12 — Editoval BakyX (30. 05. 2010 11:52)
Re: Deltoid
↑ BrozekP:
To riešenie je fakt skvelé, aj keď je trocha za ZŠ. Na ZŠ sa vzťahy medzi gonimetrickými funkciami asi nepreberajú. Ale mne to stačí. Ďakujem
Pre zaujímavosť: Dalo by sa to aj nejakým spôsobom adekvátnym k učivu ZŠ ?
1^6 - 2^6 + 3^6 = 666
Offline
#7 30. 05. 2010 13:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Deltoid
Zdravím vás,
podle Bělouna goniomerické funkce jsou probírány, úlohy s použitím gon. funkcí pro pravoúhlý trojúhelník jsou řešeny. Ale tady se mi zdá, že vzhledem k hodnotě velikosti úhlopříčky by možna stalo za to doplnit do nákresu čtverec tak, aby BD byla jeho úhlopříčka atd.
Musím ovšem momentálně umývat podlahu, tak to berte jen jako námět (v mém provedení to možna zůstane námět i nadále).
Offline
#8 30. 05. 2010 13:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ jelena:
Zdravím, tady jsem si čtverec s úhlopříčkou BD nakreslil:
Možná jsem to špatně pochopil, ale nevidím, jak by nám to mohlo pomoct.
Offline
#9 30. 05. 2010 13:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Deltoid
↑ BrozekP:
Děkuji. Tak třeba délka AX je jasná (ale já musím tu podlahu :-)
Offline
#10 30. 05. 2010 13:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ jelena:
No jo :-). Ale co s SC, případně CY?
Offline
#11 30. 05. 2010 15:17 — Editoval jelena (30. 05. 2010 15:19)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Deltoid
↑ BrozekP:
A teď bych navrchovala udělat přímku bodem C, rovnoběžně BD (vznikne trojuhelník B´YD´) a zaměřit se na podobnost trojuhelníků B´YD´a BYD.
Já se ovšem musím zaměřít na něco zcela jiného :-)
Edit: opravila jsem označení vrcholu trojuhelníku.
Offline
#13 06. 06. 2010 11:50
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ jelena:
Už jsem se dopracoval k výsledku postupem, který navrhuješ :-). (Tedy bez jakéhokoliv použití trigonometrických funkcí.)
Offline
#15 06. 06. 2010 12:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ BakyX:
Nerozumím, jak to myslíš. Výsledek je 2.
Offline
#17 06. 06. 2010 14:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Deltoid
↑ BakyX:
Pokud víš, že výsledek pro  bude
bude  , tak z podobnosti deltoidů je jasné, že obecně bude
, tak z podobnosti deltoidů je jasné, že obecně bude 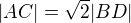 . Tak ten postup:
. Tak ten postup:
Trojúhelník BXA je rovnoramenný, proto |BX|=|XA|. |BX| ale známe, protože je to přepona pravoúhlého rovnoramenného trojúhelníku BSX. Známe tedy délku AS. .
.
Trojúhelníky DSY a D'CY jsou podobné. Platí tedy
(1)  .
.
Teď rozeberu jednotlivé délky v této rovnosti:
1) D'Y je přepona pravoúhlého rovnoramenného trojúhelníku D'CY: 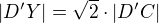 .
.
2)  . Trojúhelník CD'D je rovnoramenný, proto
. Trojúhelník CD'D je rovnoramenný, proto 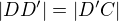 . Pokračuji ve výpočtu délky |DY|:
. Pokračuji ve výpočtu délky |DY|: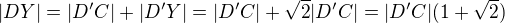
3) 
4) 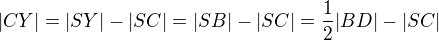
To vše teď dosadím do rovnosti (1):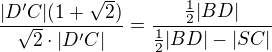
a vyjádřím |SC|.
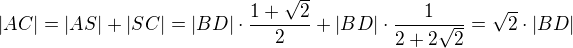
Offline
#19 31. 05. 2020 11:06 — Editoval Cenobita (31. 05. 2020 11:18)
Re: Deltoid
↑ Pavel Brožek:
α+ β + γ + δ = 360°; součet vnitřních úhlů čtyřúhelníku (zde deltoidu)
α=360°-90°-90°-135°=45°=π/4
Ještě bych si dovolil zjednodušit řešení:
tan(45°)=cotg(45°)=1
tan(π/4)=cotg(π/4)=1
|BD|=√2
t=|BD|/2
t=√2/2
x1+x2=t*( tan(α) + cotg(α) )=t*(1+1)=t*2=√2/2 * 2 = √2
t=|AC|=√2
=======
Nepočítám tak snadno jako když dýchám a někdy i chybuji.
Offline
#20 31. 05. 2020 11:10
#22 31. 05. 2020 11:20
Re: Deltoid
↑ vlado_bb:
Nejde o toho původního tazatele, ale o to, že tam byly v tom "nejlepším řešení" zbytečné goniometrické úpravy, které jsou matoucí.
Nepočítám tak snadno jako když dýchám a někdy i chybuji.
Offline