Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Fibonacciho posloupnost, řetězové zlomky a důkaz (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 06. 2010 12:20
Fibonacciho posloupnost, řetězové zlomky a důkaz
Zdravím,
nazvěme jednopatrový řetězový zlomek (možná se tomu říká jinak):  ,
,
dvoupatrový: 
třípatrový:
 , atd.
, atd.
když jsem počítal jejich hodnoty, tak to vychází:
všiml jsem si že čitatel P(1) (označme: c[P(1)]) je jmenovatelem P(2) (označme: j[P(2)]),
to mě vedlo k domněnce:![kopírovat do textarea $\rm{P}(n)=\frac{c\[\rm{P}(n)]}{c\[\rm{P}(n-1)\]}$](/mathtex/ae/aeb7c657ef24019382818cb808a28e5e.gif)
dále mě napadlo, že: ,
,
kde  značí n-té Fiboncciho číslo.
značí n-té Fiboncciho číslo.
Dokažte, nebo vyvraťte!
P.S.: Znamená to tedy, že existuje nějaká spojitost mezi Fibonacciho posloupností a speciálním případem řetězových zlomků??
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 17. 06. 2010 14:47
Re: Fibonacciho posloupnost, řetězové zlomky a důkaz
↑ byk7:
Je to tak, jak uvádíš. Když si dosadíš za m=1, dostaneš v čitateli a jmenovateli právě členy Fibonacciho posloupnosti. Pokud budeme uvažovat řetězový zlomek s nekonečně mnoha úrovněmi, v nichž jsou pouze jedničky, pak jeho hodnota je rovna tzv. zlatému řezu:
http://cs.wikipedia.org/wiki/Zlat%C3%BD_%C5%99ez
A právě zlatý řez vystupuje při explicitním vyjádření členů Fibonacciho posloupnosti.
http://cs.wikipedia.org/wiki/Fibonacciho_posloupnost
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 17. 06. 2010 17:42
Re: Fibonacciho posloupnost, řetězové zlomky a důkaz
↑ Pavel:
díky za informaci, vzhledem k Fibonacciho posloupnosti mě napadla ještě jedna úloha:
"Určete všechna  , pro která platí
, pro která platí  ."
."
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#4 17. 06. 2010 21:06
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Fibonacciho posloupnost, řetězové zlomky a důkaz
"Máte úhel beta." "No to nemám."
Offline
#5 21. 06. 2010 16:46 — Editoval byk7 (02. 07. 2010 08:35)
Re: Fibonacciho posloupnost, řetězové zlomky a důkaz
↑ Pavel:
Ještě mě napadalo, závisí hodnota zlomku na  ?
?
Pro  je situace jasná:
je situace jasná: ,
,
což dokázal tuším Kepler (?), (nevíte, kde si můžu ten důkaz pročíst?).
Ale nevím jak vyjádřit hodnotu  pro
pro  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 01. 07. 2010 13:20 — Editoval Pavel (01. 07. 2010 13:21)
Re: Fibonacciho posloupnost, řetězové zlomky a důkaz
↑ byk7:
Tady bych Tě opravil, podíl dvou po sobě jdoucích Fibonacciho čísel není roven zlatému řezu, ale limitně se k němu blíží. Tzn.
Ať mohu postupovat dál, lehce bych pozměnil Tvé značení. Nechť 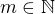 a
a


atd. Tzn.  udává počet zlomkových čar v řetězovém zlomku
udává počet zlomkových čar v řetězovém zlomku  .
.
Dosud jsme ukázali, že  .
.
Otázka je, jaká je limita  .
.
Užitím matematické indukce lze snadno ukázat, že 
Užitím věty o třech limitách dostáváme nerovnosti
tzn.
Tudíž limita je stejná jako v případě 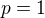 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Fibonacciho posloupnost, řetězové zlomky a důkaz (TOTO TÉMA JE VYŘEŠENÉ)

