Matematické Fórum

Ten n-rozměrný případ pro n > 2 lidsky vysvětlit neumím,  zkusím to pro n = 2 .

O funkcích f, g  dvou proměnných předpokládáme, že rovnicí g(x,y) = 0  je určena  křivka  c,  v jejímž nějakém okolí mají obě funkce
spojité parciální derivace, při čemž v každém bodě křivky c  je g'(x,y) =/= 0 .  Hledáme lokální extrém funkce f vzhledem ke křivce c.
Dejme tomu, že ten nastane v bodě W=[u,v] ležícím na c,  tedy splňujícím rovnici  g(u,v) = 0   a nerovnici g'(u,v) =/= 0 .  Poslední podmínka
znamená, že v bodě W je jedna z parc. derivací funkce g nenulová , nechť je to ta podle y .  Na funkci g v okolí bodu W aplikujeme větu
o existenci implicitní funkce h zajišťující splnění rovnic

                ,  ,

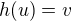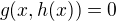(1)         

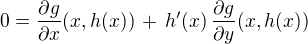
pro x z dostatčně malého okolí bodu u  (včetně bodu x=u). Lokální extrém funkce f v bodě W vzhledem ke křivce c  je tedy zároveň
lokálním extrémem funkce  F(x) = f(x,h(x)) v bodě u.  Funkce F má v bodě u derivaci, takže z nutné podmínky pro extrém funkce
jedné proměnné plyne

(2)          .

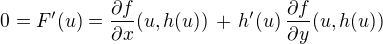Tvrzení věty o L.m. odtud dostaneme snadno přes Jacobiho determinant funkcí f, g ,   který v bodě W je roven 0, jak plyne z (1), (2).